[ 긴 글 주의 ]
삼투와 삼투압, 그리고 농도 평형
"그래서 언제까지 일어나는 건데?"
0. 들어가기
고등학교 화학2, 용액 단원에서 총괄성(colligative property)에 대해 다룬다. 학생들은 증기압 내림, 끓는점 오름, 어는점 내림, 삼투압을 차례로 배운다. 교육과정에서는 이 네 가지 개념을 두 가지 성취 기준으로 구분하여 제시한다.
과학과 교육과정(제2015-74호)
[12화학Ⅱ01-09] 묽은 용액의 증기압 내림, 끓는점 오름, 어는점 내림을 이해하고, 일상생활의 예를 들 수 있다.
[12화학Ⅱ01-10] 삼투 현상을 관찰하고, 삼투압을 설명할 수 있다.
화학2가 배추를 소금에 절이는 것과 같은 실생활 삼투 현상을 소개하고 체험하는 정도에 머무르는 교과목이라면, 위의 성취 기준을 가볍게 생각할 수도 있겠다. 그러나 화학2는 2015 개정 교육과정에서 진로 선택 과목으로 분류되며, 학교에서 실제로 어떻게 운영되든지 간에 분류상으로는 고등학교 이후 화학 관련 진로를 희망하는 학생들이 선택할 것을 염두해둔 과목이다.
이에 교과서에는 반트 호프 법칙(van't Hoff's law, Π = CRT )은 물론, 혈액의 삼투압을 구하는 예제도 실린다. 또한 국가 수준 학력평가와 모의고사에서 학생들은 U자관에서의 삼투압 계산이나 용질의 분자량 계산 등의 문제도 해결해야 한다. 개념이 명확치 않거나 오개념이 한 번 생기면 한없이 어려워지기도 한다. (글을 쓰고 있는 나 역시 어렵다. 글을 쓰는 도중에도 몇 번씩 현타가 왔다 갔다.)
이번 글을 통해서는 삼투 현상과 삼투압, 그리고 삼투 전후 용액의 농도 변화를 주로 다루고, 자칫 헷갈릴 수 있는 부분에 대해 생각해보고자 한다. 그 과정이 간단치는 않을 듯하다. (뭐 이렇게까지 하나하나 따져봐야 하나?라는 생각이 들긴 한다.)
1. 삼투 현상
삼투(osmosis)란, 농도가 다른 두 용액이 반투막*을 사이에 두고 분리되어 있을 때, 저농도 용액의 '용매' 입자가 고농도 용액 쪽으로 이동하는 현상을 말한다. 일종의 용매 확산(diffusion)이다.
여기서 반투막*(semipermeable membrane, 반투과성 막)은 <그림 1>과 같이 입자를 선택적으로 투과시키는 막이다. 일반적으로 크기가 큰 용질 입자는 통과시키지 않고, 크기가 작은 용매 입자만 통과시킨다.

1.1. 칸막이로 분리된 두 용액
다음 <그림 2>의 상황을 가정해보자.
두 용액이 칸막이에 의해 분리되어 있다. 칸막이 왼쪽에는 저농도 용액, 오른쪽에는 고농도 용액이 있다. 두 용액은 모두 이동성 피스톤에 의해 부피가 변할 수 있고, 외부압은 일정하다. 현재 두 용액은 완전히 분리되어 있으며, 각각의 계(system)로 취급된다.

1.2. 투과성 막으로 분리된 두 용액
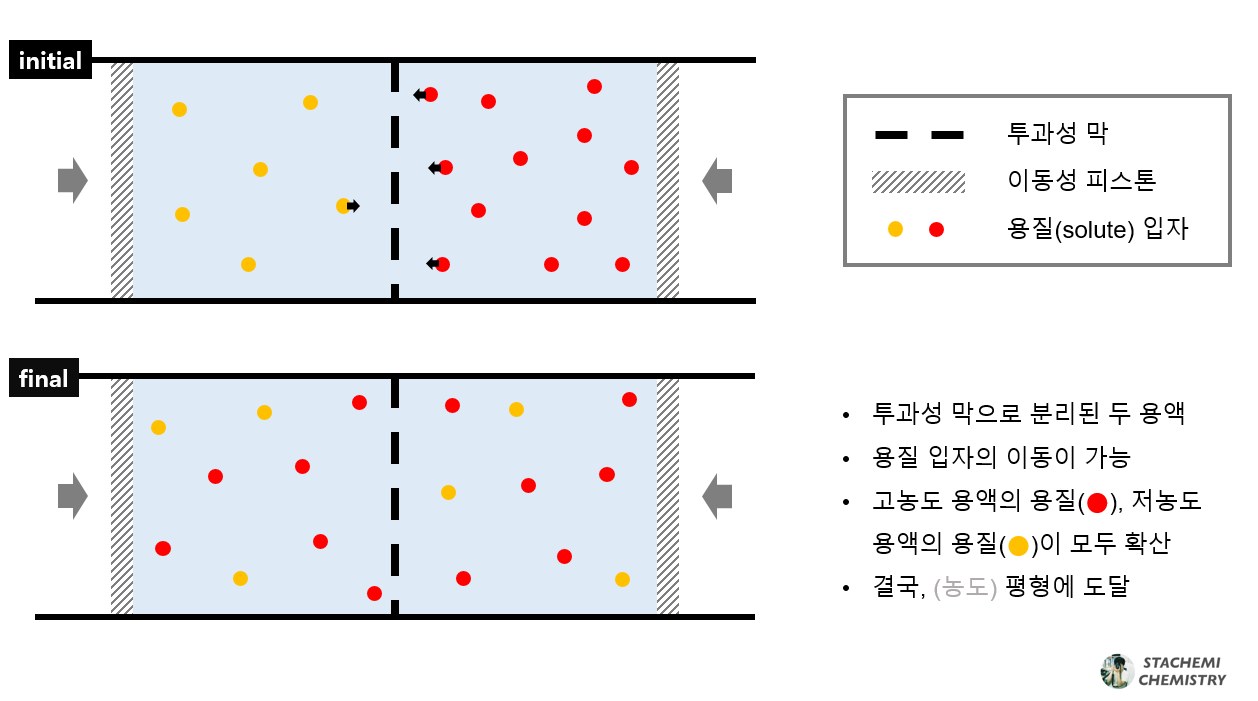
이제 <그림 3>처럼 칸막이를 투과성 막(permeble membrane)으로 바꿔보자.
두 용액은 물리적으로 연결되었다. 용매, 용질 입자 모두 막을 통과하기 때문에 막이 없는 거나 마찬가지다. 자연스러운 용매와 용질의 확산이 일어난다. 용질 입자가 골고루 퍼지고, 용액이 전체적으로 균일해지면 더 이상 알짜 흐름은 발생하지 않는다.
용액이 균일해지는 과정은 마치 콕에 의해 분리되어있던 두 기체가 섞이는 것과 같다. 기체의 확산과 다른 점은 용질 입자들이 퍼져나가는 공간이 용매 입자들 사이사이라는 점이다. 확산 전, 저농도, 고농도로 구분되던 기존 용액들은 결국 동일한 액성을 갖고, (농도) 평형 상태에 도달한다.
1.3. 반투과성으로 분리된 두 용액
만약, 가운데 막이 <그림 4>와 같은 반투막이라면?
반투막은 용질 입자에게는 칸막이(1.1.)처럼, 용매 입자에게는 투과성 막(1.2.)처럼 작용한다. 따라서 용질 입장에서는 1.1. 의 분리된 상황과 다를 바 없다. 저농도 용액의 '용질'과 고농도 용액의 '용질'은 섞일 수 없다.
그러나 '용매' 입장에서는 연결된 하나의 계이다. 기존 용액의 저농도, 고농도 구분은 용질 관점에서의 농도 표현이다. 용질이 분리되어 있는 계의 용매 확산 현상을 용질 관점으로 설명하기는 불편하다. 따라서 우리의 관심을 용매 쪽으로 옮겨오도록 하자.
용매가 용질에 녹아 용액이 만들어졌다고 생각해보자. 용매의 진하기(농도)는 기존(용질) 저농도 용액 > 기존(용질) 고농도 용액이다. 용매 관점에서 농도를 표현하면 용매 고농도 용액과 용매 저농도 용액이 되겠다. (용질) 고농도 용액에서 용질이 차지하고 있는 공간을 (용질) 저농도 용액에서 용매가 채우고 있다.
용매의 농도 차이는 '용매가 반투막에 가하는 압력 차이'를 만든다. 이 압력 차이는 용매의 알짜 흐름을 만든다. 용매 고농도 용액에서 용매 저농도 용액 방향(→)으로 향한다. 두 용액의 용매가 반투막에 가하는 압력차가 해소될 때까지 계속된다. 그리고 압력차가 해소되었을 때, 두 용액의 농도 또한 같아진다.
정리하자면, 용매의 알짜 흐름은 압력 차이에 의해 나타나고, 그 압력 차이는 용액의 농도 차에 의한다.

1.4. 반투과성 막으로 분리된 용매와 용액
만약, <그림 4>의 저농도 용액이 그냥 순수한 용매(물)이라면 어떨까? 용액은 한 종류밖에 없으니 이때의 삼투 현상은 두 용액 간의 상대적인 농도 차이가 아닌, 용액의 절대적 진하기에 의존하는 압력으로 취급할 수 있다.
Π = CRT
<그림 5>의 용매는 일종의 극단적인 저농도 상황을 가정했다고 생각해도 좋다. 용매와 용액 사이에 압력차가 해소될 수 있을까? 용매의 알짜 흐름이 사라지고, (농도) 평형에 도달할 수 있을까?


초기 용액의 농도는 삼투압을 발생시키고, 용매의 알짜 흐름을 만든다. 용매는 용액 쪽으로 이동하고, 용액의 농도는 점점 묽어진다. 용액이 묽어질수록 용매와의 농도 차이는 줄어들지만 용매가 남아 있는 한 차이가 사라질 수는 없다. 계속 묽어지겠지만, 용액은 결코 순수한 용매가 될 수 없다.
결론은 모든 용매가 용액 쪽으로 이동해야만 알짜 흐름이 사라진다. 어쨌든 단일 농도이긴 한다.
"만약, 순수한 용매가 전혀 이동하지 않고, 초기 상태를 그대로 유지하게 하려면 어떻게 해야 할까? 아마도 용액 쪽에 여분의 압력이 가해져야만 할 것이다." 우리는 이때 필요한 여분의 압력을 삼투압(osmotic pressure, Π)으로 정의한다.
2. U자관에서의 삼투 현상
잡담 주절주절...
사실, 이 주제로 포스팅을 하겠다고 마음먹음과 동시에 다소 생소한 이동식 피스톤으로 막힌 모형을 굳이 사용한 이유는 모두 U자관에서의 삼투 때문이다.
몇 달 전, 2021 MDEET 문제 풀이(148)에서 U자관에서의 삼투압을 다룬 적 있었지만, 접근성이 떨어져서 미래의 나는 분명 찾지 못할 것이라는 것을 알고 있었다.
그래서 꼭, 따로 정리해두어야 한다는 생각을 했었다. 그러나 막상 쓰려니 엄두가 나지 않아 실천에 옮기지는 못했는데, 며칠 전, 교과연구회 선생님들과 우연히 삼투압을 주제로 대화하게 되어 생각난 김에 관련 내용을 정리할 겸 무작정 글쓰기를 시작해버렸다. (엄청 후회 중이다.)
우리는 보통 U자관을 이용해 삼투 현상을 설명한다. <그림 6>과 같이 칸막이로 나뉜 수조에 반투막을 설치한 장치를 쓰기도 하는데, 이 또한 모양만 다른 U자관이다.

삼투 현상 설명에 U자관을 쓰는 이유는 너무나 명확하다. 생소한 물리 개념인 삼투압을 관찰(측정) 가능한 형태로 바꿔주기 때문이다. 반투막이 받는 압력차라는 말은 쉽게 와닿지 않지만, 용액의 높이차를 보여주는 것은 직관적이다.
삼투에 의한 높이차 해소를 위해 높은 쪽 수면을 눌러주어야 하며, 이에 추가적인 압력이 필요하다는 설명도 쉽게 이해할 수 있다.

(a) 초기 높이가 같은 농도가 다른 두 용액이 반투막을 사이에 두고, 놓여 있다. 용액의 농도차로 인해 저농도 용액의 용매가 고농도 용액 쪽으로 이동한다.
(b) 용매 이동이 시작되면, 두 용액 사이에는 높이 차가 발생한다. 그리고, 알짜 이동이 없는 평형 상태에 도달한다. 두 용액의 높이차에 해당하는 물기둥이 가하는 압력은 ρgh 로 손쉽게 구할 수 있다.
(c) 발생한 높이차를 (a)처럼 되돌리기 위해 가해져야 하는 여분의 압력이 삼투압(Π)이다.
위의 설명 과정에는 아무런 문제가 없다. 그런데, 곰곰이 생각하다 보면, 이전에 생각하지 못했던 몇 가지 궁금한 점들이 생긴다.
2.1. U자관에서의 삼투압의 크기?

U자관 반투막을 기준으로 왼쪽에 저농도(C1), 오른쪽에 고농도(C2) 용액이 연결되어 있다. 두 용액의 농도 차에 의해 발생하는 용매 이동을 막기 위해서는 <그림 8>의 (가)처럼 외부에서 추가적인 압력(P0)이 반드시 필요하다. 정의상 이때 필요한 압력은 두 용액의 삼투압 차이다. 그 크기는 얼마일까?
C1 용액과 C2 용액 각각이 반투막을 사이에 두고, 순수한 물과 연결되었다 생각하면 C1의 삼투압 Π1 = C1RT 이고, C2의 삼투압 Π2 = C2RT 이다. 따라서 농도가 진한 C2 용액의 삼투압이 더 크고, 순수한 물의 이동을 막기 위해 가해주어야 하는 압력이 더 크다. (Π2 > Π1)
따라서 두 용액을 (가)와 같이 연결하면 농도 차이만큼의 삼투 현상이 발생할 것이며, 이를 억제하기 위해서는 C2 용액 쪽에 압력을 가해주어야 한다. (가)에서 나타낸 압력의 크기는 P0 이다.

즉, 두 용액의 삼투압 차이(= (C2 - C1)RT )만큼의 압력인 P0 를 가해야만 용매의 이동을 완전히 막을 수 있다.
2.2. 결국, 용액의 농도는 같은 거야? 다른 거야?
<그림 8> (가)의 P0 를 제거하면, 저농도(C1) 용액의 용매가 고농도(C2) 용액 쪽으로 이동한다. 용매가 이동함과 동시에 양쪽 수면 높이는 달라진다. <그림 8> (나)와 같이 용매가 유입된 고농도 용액 쪽 수면이 높아지는 만큼, 저농도 용액 쪽 수면이 낮아진다.
처음 C1, C2였던 두 용액의 농도도 C1', C2' 로 변한다. C1'은 이전(C1)보다 진해지고(C1' > C1), C2'은 이전(C2)보다 묽어졌을 것(C2' < C2)이다.
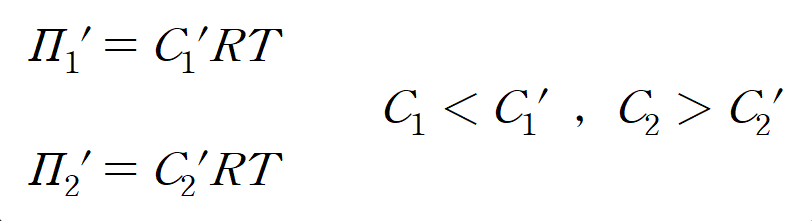
평형에 도달한 두 용액의 농도(C1', C2')는 어떨까? 같을까? 결론부터 말하면, C1' , C2'은 다르다. U자관에서는 농도가 같아질 때까지 용매 이동이 일어날 수 없다.
C1(저농도) 용액 용매가 C2(고농도) 용액 쪽으로 이동한다. C1 용액 부피가 줄어드는 만큼 C2 용액 부피가 늘어난다. 이동한 용매는 고농도 용액 쪽에 물기둥(정확히는 C2' 용액 기둥)을 쌓는다. 물기둥은 높이차만큼의 압력을 만들어낸다. 높이차에 의해 압력 발생한다는 점이 앞선 이동성 피스톤 모형(1.3.)과 다른 점이다.
쌓이는 물기둥은 삼투 현상 반대 방향(↓)으로 압력을 가하며, 이는 삼투압 차이에 의한 용매의 자연스러운 이동을 방해한다. 즉, 물기둥이 없는 위의 피스톤 모형일 때보다 용매의 알짜 흐름이 적어질 수밖에 없다.
용매가 이동하고, 시간이 흐를수록 점점 두 용액의 농도가 비슷해진다. 또한 물기둥은 점점 높아지고, 물기둥이 용매의 이동을 방해하는 힘 또한 커진다. 결국, 쌓인 물기둥의 압력(=ρgh)이 C1', C2' 용액의 농도차에 의한 삼투압 크기(Π')와 같아지면, 더 이상 용매는 이동할 수 없다.
용매 이동 초반에는 농도차에 의한 삼투압 > 물기둥의 압력보다 크기 때문에 용매의 알짜 흐름이 발생하지만, 농도차가 줄면서 삼투압 크기는 작아지고, 물기둥의 압력은 점점 커지기 때문에 결국 두 압력이 같아지는 시점이 생긴다.
"두 용액의 농도차에 의한 삼투압만 생각하면, 아직까지 알짜 흐름이 있어야 하지만, 반대로 작용하는 물기둥 압력에 의해 용매 이동이 가로막히면서 두 용액은 (압력) 평형에 도달한다."

따라서 "U자관에서 높이차가 존재하는 한(h ≠ 0) 두 용액의 농도는 같을 수 없다(C2' ≠ C1'). 또한 물기둥의 높이차가 클수록 평형에서의 두 용액 사이 농도 차이(C2' - C1')도 크다."
* 다른 관점으로 생각해보기
1) 최초, 저농도 C1 용액에서 고농도 C2 용액으로 용매가 이동하여 수면에 높이차가 생기면, 즉각적으로 생겨난 높이차만큼의 C2 용액을 덜어내자. 다시 양쪽 용액의 수면이 맞춰졌다. 용매의 이동으로 인해 두 용액의 농도는 초기보다 조금 비슷해졌다.
2) 하지만, 농도차가 존재하는 한 저농도 C1 용액은 고농도 C2 용액 쪽으로 계속 이동하려 할 것이다. 용매가 이동할 때마다 물기둥이 쌓이지 않도록 용액을 덜어내어 수면의 높이를 계속 맞춰주자.
3) 만약, 용액을 덜어내지 않았음에도 높이차가 발생하지 않는다면, 더 이상 용매의 알짜 흐름이 없다는 말이다. 두 용액이 농도 평형에 도달했다는 뜻이기도 하다. 양쪽 수면의 높이도 동일하다.
3) 이제, U자관 속 용액과 동일한 농도 용액을 한쪽에만 넣어 준다면 어떻게 될까? U자관 한쪽에만 추가로 압력을 가하는 행위다. 이미 두 용액은 농도 평형에 도달한 상태였고, 첨가한 용액의 농도가 같으므로 농도차에 의한 삼투압은 생기지 않는다(C1" = C2"). 그저 외부에서 넣은 용액이 만드는 용액 기둥 높이에 해당하는 압력이 생긴 상황이다.
4) 첨가된 용액 기둥의 압력 때문에 용매 흐름이 반대쪽(C2" → C1")으로 생긴다. 이로 인해 두 용액은 다시 농도 차이가 발생한다. 용액의 농도차가 점점 벌어지다가, 농도차에 의한 삼투압의 크기(→)와 수면 높이차에 해당하는 물기둥의 압력 크기(←)가 같아지면, 용액의 알짜 흐름이 생기지 않는다. 용액의 농도는 C1', C2'이 되며, C2'가 C1'보다 조금 진한 상태일 것이다.
삼투압(농도차 = C2' - C1')에 의한 용매 이동 → |반투막| ← 용액 기둥(=ρgh)에 의한 용매 이동
2.3. 용액 높이차에 해당하는 압력(ρgh) = 삼투압(ΔCRT)일까?

위의 <그림 8>을 다시 가져왔다.
(가)의 P0는 C1 용액의 용매가 C2 쪽으로 전혀 이동하지 못하도록 가하는 압력이다. 두 용액의 초기 농도차에 의한 삼투압에 해당한다.
(나)의 용액 기둥의 압력 ρgh 는 용매의 알짜 이동이 더 이상 일어나지 않는 평형에 도달했을 때의 압력이다. 두 압력의 크기는 같을까?
"(엄밀하게는) 다르다."
(나)는 아직 두 용액의 삼투압 차이가 완전히 해소되지 않았다. 농도가 같아질 때까지 용매가 이동하지 못했다. 층층이 쌓인 용액 기둥이 가하는 압력 때문에 더 일어났어야 할 용매 이동이 저지당한 상태다. 따라서 용액 기둥이 없다면, C1'에서 C2' 방향으로 추가적인 알짜 흐름이 발생한다. 이 잠재적인 흐름에 해당하는 삼투압의 크기가 (C2' - C1')RT 이며, 이것을 막고 있는 용액 기둥의 압력 ρgh 와 같은 상태다.
반면, (가)의 P0는 초기 용액의 농도차가 만들어내는 압력의 크기다. 즉, (C2 - C1)RT 이다. 초기 C2의 농도는 C2'보다 진하며(C2 > C2'), C1의 농도는 C1'보다 묽기(C1 < C1') 때문에 언제나 P0 > ρgh 를 만족한다.
2.4. 그런데, 왜?
2.3. 에서 살펴본 바와 같이 U자관에서 용액의 높이차에 해당하는 용액 기둥의 압력(ρgh )보다 삼투압(Π)이 더 큼에도 왜 두 압력을 동일한 것처럼 취급할까?
사실 엄밀하게는 두 용액의 높이차(또는 물기둥의 압력)는 (초기 농도차에 의한) 삼투압에 비례한다 정도가 올바른 표현일 것 같은데 말이다.

위의 <그림 7>에서도 (b)의 높이차에 해당하는 압력을 그냥 삼투압(osmotic pressure)이라고 표현했으며, (c)에서 수면을 일치시키기 위해 필요한 압력의 크기가 (b)의 압력과 같다고 표현했다.
.
(b)의 용액 기둥 압력과 (c)의 삼투압 사이의 압력 차이(ΔP = P0 - Π ')를 식으로 나타내면 다음과 같다.

사실, 우리가 지금껏 사용해온 반트 호프 식(Π = CRT ) 식은 용매와 용액의 화학 퍼텐셜 관계로부터 이끌어낼 수 있는데, 매우 묽은 용액이라는 전제 하에 이루어진다. (용액의 총괄성에 관련된 식에 모두 비슷한 근사 과정이 포함된다.)
[참고] 관련 글 : 반트 호프 식의 증명(191)
따라서 우리가 본문에서 고농도 용액이라고 표현은 했지만, 기본적으로 절대 농도가 매우 묽은 상태(C2 ∽ 0)로 상황이 설정된다 생각하면, 용매 이동 전후의 진한 용액의 농도차이(C2 - C2') 또한 매우 작을 것으로 기대할 수 있다.
즉, 매우 묽은 용액과 순수한 물(C1=0) 사이에서 (b)의 용액 기둥 압력(Π ')과 (c)의 삼투압(P0)의 크기를 비교한다면, 그 차이가 적어 설명의 용이성을 위해서라도 굳이 두 압력을 굳이 구분하지 않는 것은 아닐까?
3. 마치며...
글을 비공개 발행(저장) 한 것이 11월 16일이다. 그리고 지금은 11월 22일이다. 그냥 대략적인 내용만 작성하여 임시 저장 형태로 보관했던 기간까지 합치면, 일주일이 넘게 걸린 셈이다.(그런데 문맥도 안.. 맞...) 그림 자료도 만들고, 근거도 찾아보고, 다듬고, 의심하고, 주변에 질문도 하고, 생각도 골똘히 해봤다.
그런데, 맘먹고 주저리주저리 길게도 써 내려간 본문의 설명이 올바른 것인지 확신이 서질 않는다.
사실, 대부분의 사람들은 본문 내용에 크게 관심이 없다. 그냥 삼투압이면, 반트 호프 식에 대입해서 분자량 구하고, 삼투압 구하면 되지. 그 초기 농도에 의한 삼투압 크기와 물기둥의 높이에 해당하는 압력 크기가 같은지 다른지 크게 관심 없다.
그런데 난 그런 게 궁금하고, 제대로 알지 못하는 게 스스로 찝찝하다. 그래서 이러고 있나 보다. 화학 고수가 정말 우연히 이 글을 보고, "이건, 이런 겁니다. 저건 잘못되었습니다."하고 알려줬으면 좋겠다.
삼투와 삼투압, 그리고 농도 평형 -끝-
* 긴 글, 부족한 글 읽어주셔서 감사합니다. 내용 중 오류나 잘못된 설명 등이 있는 경우 댓글로 알려주시면 너무 감사드리겠습니다.
* [수정] 2025-09-03 용액의 기둥과 삼투압 사이의 압력 차이 관련 수식 이미지 수정 [댓글 참고]
[그림 7 출처] https://2012books.lardbucket.org
Colligative Properties of Solutions
13.5 Colligative Properties of Solutions Learning Objective To describe the relationship between solute concentration and the physical properties of a solution. Many of the physical properties of solutions differ significantly from those of the pure substa
2012books.lardbucket.org
[그림 8 관련 문항 풀이(7번)] https://stachemi.tistory.com/148
2021 MEET/DEET 자연과학2(일반화학) 기출문제 풀이 (6번-10번)
<이전 글> 2021 MEET/DEET 자연과학2(일반화학) 풀이 1번~5번 : https://stachemi.tistory.com/146 2021 MEET/DEET 자연과학2(일반화학) 기출문제 풀이 (1번-5번) 주절주절... 노량진에서 외로이 임용고시를 준..
stachemi.tistory.com
'화학 > 화학이야기' 카테고리의 다른 글
| 분자 궤도함수 이론 (Molecular Orbital Theory, MOT) (2) | 2020.11.27 |
|---|---|
| 반트 호프 식 (van't Hoff equation) - 묽은 용액의 삼투압 (2) | 2020.11.24 |
| 두 종류의 반응물로 이루어진 2차 반응 (3) | 2020.11.09 |
| 화학 반응의 속도 (6) | 2020.11.07 |
| [화학 실험] 파라오의 뱀 (Pharaoh's Serpent) (0) | 2020.11.05 |



