상 경계 (Phase Boundary)
앞선 상 전이의 열역학적 양상에 대한 글을 통해 상 변화 과정에서의 깁스 자유에너지(화학 퍼텐셜) 변화를 살펴보았으며, 압력 변화와 온도 변화 두 가지 요인에 의한다는 것을 알게 되었다. 특히 일정 압력 하에서 온도 변화에 따른 깁스 자유에너지는 그 상의 엔트로피에 의존하며, 일정 온도 하에서 압력 변화에 따른 깁스 자유에너지는 그 상에 몰부피에 의존함을 알게 되었다. 이번에는 상 전이 도표 상에서 상 경계가 갖는 의미가 무엇인지를 살펴보고, 액체-기체, 고체-액체, 고체-기체 상 변화에서 상 경계가 갖는 특징을 살펴보고자 한다.
1. 액체-기체 상 경계
다음 그림은 물의 상 경계를 보여주는 그래프이다. 특히 물과 수증기(액체와 기체) 사이 상경계 곡선 위의 압력 값은 해당 온도에서의 액체의 증기압(vapour pressure)이다.

액체-기체 상 경계는 액체 상과 기체(증기) 상이 동적 평형을 이루고 있는 온도와 압력을 연속적으로 나타낸 것이다. 우리는 액체와 그 액체의 증기가 평형을 이룰 때, 증기가 갖는 압력을 증기압으로 정의한다. 따라서 상 도표상의 액체-기체 상 경계를 나타내는 곡선은 액체의 증기압 곡선이기도 하다.
온도가 높아질수록 액체의 증기압은 커진다. 20 ℃의 물은 0.023 atm의 수증기와 평형을, 100 ℃의 물은 1 atm의 수증기와 평형을 이룬다. 만약 해당 기체의 증기압이 이에 미치지 못하면, 액체 내부에서 끓음(boiling)이 발생한다. 액체 내부에서도 기포가 보글보글 생성된다.
액체-기체 상 경계는 액체 상과 기체 상이 평형을 이루고 있는 온도와 압력이다. 두 상이 평형을 이루고 있다는 것은 두 상의 자유 에너지가 같다는 것이다. 100 ℃의 물과 100 ℃의 수증기는 같은 자유 에너지를 갖는다. 만약 평형을 이룬 이 계의 온도를 0.1 ℃ 상승시킨다면 순간적으로 평형이 깨지고, 평형을 유지하기 위해 액체는 증기를 더 생성할 것이다. 100.1 ℃에 해당하는 증기압을 만족할 때까지 증기를 생성한다. 그리고 다시 액체와-기체 사이 평형을 유지한다. 매 순간 평형을 만족하면서 온도를 증가시키는 것은 상도표의 상 경계 곡선을 따라 오른쪽으로 이동한다는 의미다.
-
정리하자면 두 상의 온도와 압력이 미소하게 변하는 경우 매 순간 평형을 유지하게 되는데, 이는 결과적으로 상경계를 따라 변하게 된다. 미소한 두 상의 깁스 자유에너지 변화(dG)는 매 순간 동일하다. 액체의 깁스 자유에너지가 "a"만큼 변하면, 기체의 깁스 자유에너지도 "a"만큼 변해야 한다. 그래야 매 순간 평형(Gliquid = Gvapour)을 만족한다. 이를 식으로 나타내면 다음과 같다.

이를 정리하면, 액체-기체 상경계 그래프의 기울기(dP/dT )가 어떤 의미를 갖는지 알 수 있다.

위의 온도 변화에 대한 압력 변화(dP/dT ) 식을 클라페롱(Clapeyron) 식이라 한다. 이 식을 통해 온도와 압력에 대한 상 도표의 액체-기체 상경계의 기울기는 액체에서 기체로 상 전이하는 과정에서의 부피 변화(△V, 증발 부피)와 엔트로피 변화(△S, 증발 엔트로피)에 따라 결정된다는 것을 보여준다. 액체의 기화 엔트로피 변화(△S )는 기화 엔탈피 변화(△H )를 끓는점(T )으로 나누어 구할 수 있다. 그런데 대부분의 액체는 기화될 때 유사한 몰 증발 엔트로피를 갖는다.

* 트루톤 규칙(Trouton's Rule)
일정한 압력에서 액체가 기체로 상 전이할 때, 대부분의 액체가 거의 비슷한 몰 증발 엔트로피를 갖는다는 규칙이다. 대략 10.5R J/mol·K 정도의 값을 갖는다. 여기서 R은 기체 상수이다. 약 88±5 J/mol·K 의 값을 갖는다. (단, 물, 에탄올 등 수소 결합을 하는 물질의 경우 큰 몰 증발 엔탈피 값으로 인해 예외성을 갖는다.)
[참고] https://en.wikipedia.org/wiki/Trouton%27s_rule
Trouton's rule - Wikipedia
Enthalpies of melting and boiling for pure elements versus temperatures of transition, demonstrating Trouton's rule Trouton's rule states that the entropy of vaporization is almost the same value, about 85–88 J/(K·mol), for various kinds of liquids at
en.wikipedia.org
이것을 클라페롱 식에 대입하면 다음과 같다.

그런데 액체의 몰부피는 기체의 몰부피와 비교했을 때, 무시 할 정도로 작기 때문에 기화 과정에서의 부피 변화(△V )는 기체의 몰부피와 같다. 그리고 기체의 몰부피는 이상기체상태방정식을 통해 압력과 온도를 사용하여 나타낼 수 있다.

이를 위의 식에 대입하면, 다음과 같은 클라우지우스-클라페롱(Clausius-Clapeyron) 식을 얻게 된다.

(1/P )dP = d lnP 이므로, 만약 기화 엔탈피가 온도에 대한 함수가 아니라면 다음과 같이 적분할 수 있다.

이 식을 통해 온도에 따른 증기 압력 변화와 압력에 따른 끓는점 변화를 예상할 수 있다.
2. 고체-액체 상 경계
상 도표에서 액체-고체 상 전이 과정 역시 액체-기체 상 전이와 다르지 않다. 액체가 고체로 어는 과정, 고체가 액체로 녹는 과정에서의 평형이다. 역시 이 과정에서의 엔트로피 변화(△S )는 물질 1몰이 녹을 때의 가역적인 융해 엔탈피 변화(△H )와 녹는점(T )으로 나타낼 수 있다.

액체가 증발할 때, 고체가 녹을 때 엔트로피는 증가한다. 온도 T에서 클라페롱 식은 다음과 같다.

고체-액체 사이의 상 변화 과정에서 부피 변화는 거의 없다. 대부분의 일반적인 경우 고체에서 액체로 변하는 과정의 부피 변화는 매우 작은 양의 값(△V > 0)이다. 따라서 클라페롱식의 분모가 매우 작은 값을 갖게 되며, 고체-액체 상 경계 기울기(dP/dT )는 매우 큰(가파른) 양의 값을 갖는다. 반면 얼음이 물로 녹는 과정은 예외적으로 부피가 감소하며, 고체-액체 상 경계 기울기가 음의 값을 갖는다.
3. 고체-기체 상 경계
고체-기체의 경우는 앞선 경우와 같이 다음의 식이 적용된다.
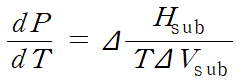
일반적으로 승화 엔탈피가 증발 엔탈피보다 크기 때문에 승화 곡선과 증기압력 곡선이 만나는 온도가 비슷한 부근에서의 기울기를 비교하면, 승화 곡선의 기울기가 더 크다.
[참고] 상전이의 열역학적 양상 http://stachemi.tistory.com/48
상 전이의 열역학적 양상 (Thermodynamic Aspects of Phase Transitions)
상 전이의 열역학적 양상 (Thermodynamic Aspects of Phase Transitions) 앞선 상평형 그림(Phase Diagram)에서 상 전이에 대해 간략하게 언급하였다. 상 전이(Phase Transition)란 어떠한 물질이 하나의 상태에..
stachemi.tistory.com
'화학 > 화학이야기' 카테고리의 다른 글
| 화학사 이야기 - 플로지스톤설 (phlogiston theory) (0) | 2020.05.26 |
|---|---|
| 몰과 아보가드로수 (mole & Avogadro's Number) (4) | 2020.05.07 |
| 반 데르 발스 기체식과 임계상수 (23) | 2020.04.12 |
| 수소꼴 원자의 슈뢰딩거 방정식 풀이 (2) (3) | 2019.12.23 |
| 수소꼴 원자의 슈뢰딩거 방정식 풀이 (1) (0) | 2019.12.12 |



