* 연관된 글 : stachemi.tistory.com/192
분자 궤도함수 이론 (Molecular Orbital Theory, MOT)
[알림] * 원자가 결합 이론(VBT)과 분자 궤도함수 이론(MOT)의 차이에 대한 일반화학 수준의 글입니다. Schrodinger 파동 방정식을 분자에 어떻게 적용했는지에 주목하여 작성한 글이며, 구체적인 분자
stachemi.tistory.com
LCAO 분자 오비탈 (LCAO Molecular Orbital)
"MO와 LCAO-MO"
1966년, 로버트 멀리컨(Robert S. Mulliken, 1896-1986)은 《chemical bond and the electronic structure of moleculaes by the molecular orbital method, 분자의 화학결합 및 전기적 구조에 관한 연구》에 대한 연구 성과를 인정받아 노벨 화학상을 수상했다. 그는 노벨상 수상 강연 《Spectroscopy, molecular orbitals and chemical bonding》에서 다음과 같이 말한다.
I have always felt that a true AO or MO for an electron is one which corresponds to a self-consistent field as above described. Commonly, however, the word orbital is used to refer to mathematical functions which are only approximations to these true AO's or MO's. The main reason for this fact is that until recently we have had in most cases, especially for MO's, only a rather roughly approximate knowledge of the true forms. In the case of MO's, the so-called LCAO approxomations are rather generally familiar.
나는 앞서 설명한 바와 같이 전자에 대한 진정한 원자 오비탈(AO), 분자 오비탈(MO)은 자체 일관성 장(SCF, self-consistent field )에 해당할 때만이라고 생각한다. 그러나 오비탈(궤도함수)라는 용어는 수학적 근사를 통해 얻어진 원자 혹은 분자 오비탈에 더 자주 쓰인다. 이런 사실의 주된 이유는 최근까지도 우리가 (원자 또는 분자의) 실제 형태에 대해 대략적인 지식만 가지고 있기 때문이다. MO의 경우 LCAO 근사법에 의한 결과(LCAO-MO)가 우리에게 보다 친숙하다.
- 1966년, 로버트 멀리컨 노벨상 강연 중에서 -
[보충 설명, 2024-7-13 추가]
위에서 로버트 멀리컨이 강연에서 지적한 것은 무엇일까?
슈뢰딩거 파동방정식을 이용하여 정확한 분자의 파동함수를 구하기 위해서는 1-전자계로 이루어져야 한다. 즉, 전자가 2개인 H2 분자의 파동함수 조차 정확하게 구해낼 수 없으며, 어쩔 수 없이 근사(approximation)를 해야 한다. 적절한 근사 방법을 통해 전자를 하나 둘씩 추가해 나가면 전자가 여럿 있는 다전자 분자의 오비탈(MO)을 완성할 수 있다.
다전자 분자의 정확한 분자의 파동 함수(MO)를 구할 수는 없다지만, 그나마 엄밀한 방식은 있다. 더글라스 하트리(Hartree)와 블라드미르 폭(Fock)가 제안한 자체 일관성 장(SCF) 이론을 바탕으로 계산하면 다전자로 이루어진 분자의 오비탈을 계산을 통해 구할 수 있다.
그런데 이 과정이 상당히 복잡하고, 반복적인 계산이 필요하기에 대부분의 사람들은 조금 덜 엄밀한 수학적 근사를 통해 분자의 오비탈을 구한다. 이 방법이 원자 오비탈의 선형 결합(LCAO)이다. 멀리컨은 SCF에 의해 계산된 결과만이 진정한 분자 오비탈(MO)이라는 견해이지만, 대부분의 사람들은 LCAO 근사법을 통해 구한 결과값을 분자 오비탈(MO)로 받아들이는 경우가 많고, 보다 친숙하게 여긴다는 것을 지적한 것이다.
1. 원자 오비탈 선형 조합 근사법(LCAO Approximation)
앞선 글(192)을 통해 Schrodinger 파동 방정식이 어떻게 분자에 적용될 수 있는지, H2+ 이온을 예로 알아보았다. 가장 단순한 분자이지만, 파동 방정식의 해(파동 함수)를 찾는 과정은 그다지 간단치 않다. 이에 전자가 여러 개인 복잡한 다전자 분자의 궤도함수를 찾기 위해 근사법에 의존하는 것이 어찌 보면 당연한 일이다.
LCAO-MO는 가장 널리 알려진 분자 궤도함수 근사법이다. 풀어쓰면 원자 오비탈 선형 조합(Linear Combination Atomic Orbital)이다. 분자를 구성하는 원자 오비탈 간의 더하기, 빼기 조합으로 분자 오비탈을 나타내는 근사법이다.
원자 A와 B가 결합해서 만들어진 간단한 이원자 분자의 파동함수는 LCAO-MO를 통해 다음과 같이 표현된다.
Ψ LC-MO = CAψA ± CBψB
여기서 대문자 프사이(Ψ )는 분자 오비탈(MO)이고, 소문자 프사이(ψA , ψB )는 원자 오비탈(AO)이다. CA, CB는 변환 계수로 각 원자 오비탈이 분자 오비탈에 기여하는 정도를 나타낸다. 만약 A와 B에 1s, 2s, 2p 등 여러 종류의 AO가 존재한다면, 각 오비탈의 기여도를 고려하여 선형 조합을 이어나가면 된다.
각각의 AO는 파동 함수(wave function, ψ )이므로, 이들의 덧셈 또는 뺄셈(선형 조합)에 의해 만들어지는 MO는 원자 A, B의 파동 간 보강 혹은 상쇄의 결과(Ψ )라 할 수 있겠다.
2. 결합성 궤도함수(bonding MO)와 반결합성 궤도함수(antibonding MO)
바닥상태 수소 원자는 1s 오비탈(ψ1s)만으로 전자 상태를 나타낼 수 있다. 따라서 이런 수소 원자들 간 결합으로 만들어진 H2 는 1s 오비탈 끼리의 보강 또는 상쇄의 경우만 있기 때문에 MO 근사법의 가장 간단한 예가 된다. 식으로 나타내면, 다음과 같다.
Ψ H2-MO = CAψA(1s) ± CBψB(1s)
H2의 파동함수(Ψ )는 두 원자 HA와 HB 파동함수(ψ )의 덧셈(+) 또는 뺄셈(-)으로 연결되었다. H2는 동핵 이원자 분자(homonuclear diatomic molecule)이므로 각 AO의 기여도가 같을 것이다.(CA = CB)
부호(±)에 따라 2 가지 MO가 가능하다. 덧셈으로 연결된 식(ψA + ψB)은 배향이 같은 두 1s 오비탈의 중첩, 뺄셈으로 연결된 식(ψA - ψB)은 배향이 서로 반대인 두 1s 오비탈의 중첩이다. <그림 1>

배향이 같은 1s 오비탈의 중첩은 두 파동 사이 보강 간섭(constructive interference)을 일으키고, 결과적으로 핵 사이 전자 밀도를 증가시킨다. 핵 사이 전자 밀도가 증가했다는 것은 각각의 원자로 존재할 때보다 결합성을 갖는다는 뜻이다. 이 오비탈을 결합성 오비탈(bonding MO, 결합성 궤도함수)이라 한다.
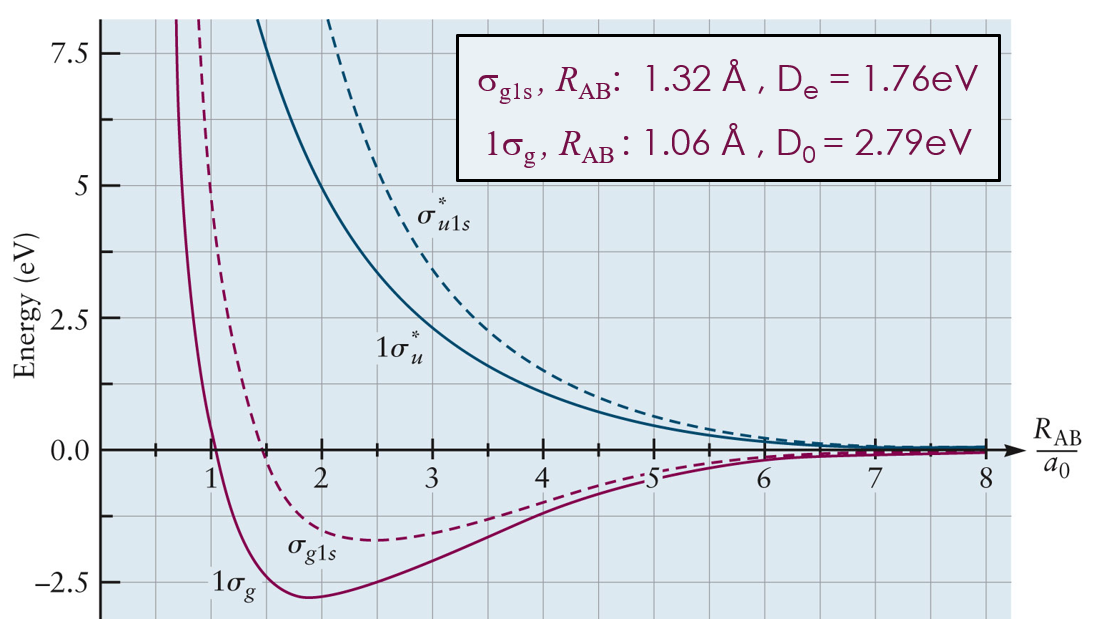
이렇게 배향이 같은 1s 오비탈 간 선형 결합을 통해 얻은 LCAO-MO는 σg,1s 로 표기하는데, 이는 파동 방정식을 통해 얻은 H2+ 실제 MO의 1σg 와 모양이 유사하다.
Ψ H2-MO = C (ψA(1s) + ψB(1s)) = σg,1s ≒ 1σg
반면, 배향이 다른 두 1s 오비탈의 중첩은 상쇄 간섭(destructive interference)을 일으켜 인해 핵 사이 전자 밀도를 감소시킨다. 결과적으로는 핵 사이 전자 밀도가 0인 마디(node)가 생기며, 이는 핵 간 반발 에너지를 증가시켜 원자 간 결합을 방해한다. 이 오비탈을 반결합성 오비탈(antibonding MO, 반결합성 궤도함수)이라 한다.
마찬가지로 배향이 서로 다른 1s 오비탈 간 선형 결합을 통해 얻은 LCAO-MO는 σu,1s*로 표기하며, 이는 실제 MO의 1σu*와 모양이 유사하다.
Ψ H2-MO* = C (ψA(1s) - ψB(1s)) = σu,1s* ≒ 1σu*
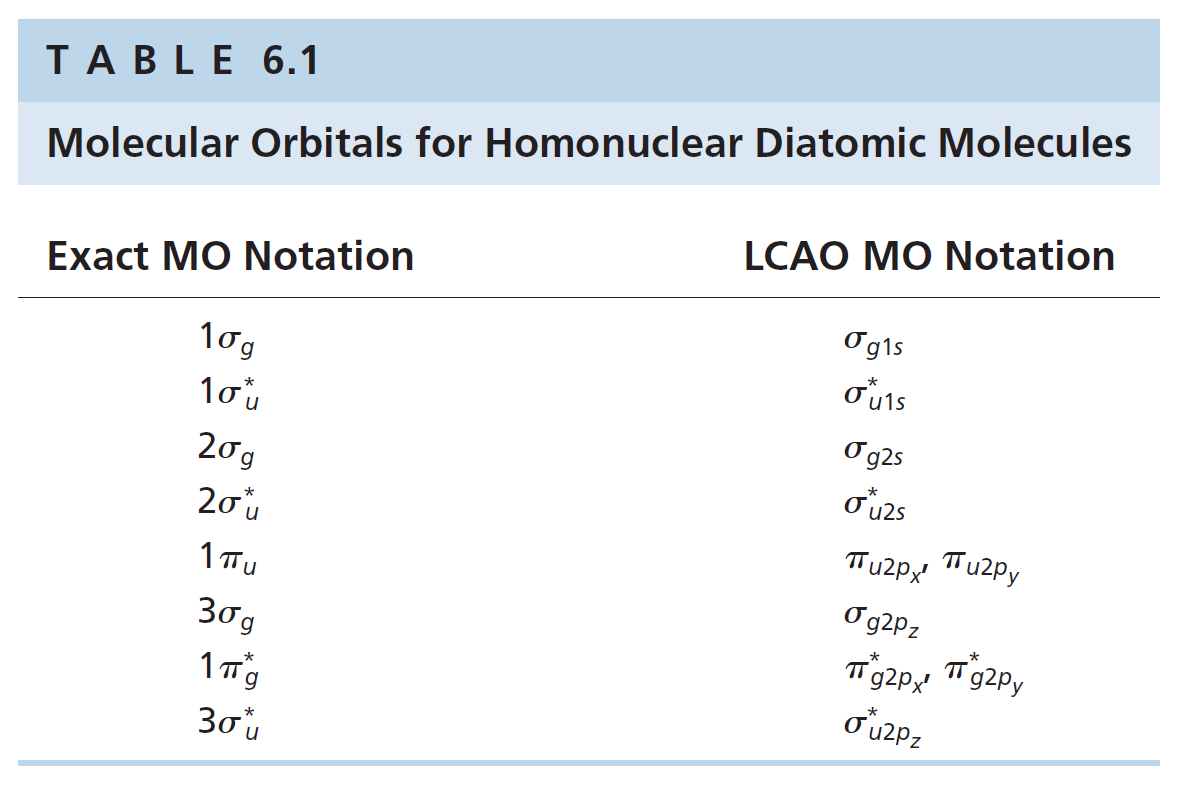
3. 분자 궤도함수 에너지 도표
LCAO 근사법을 통해 구성된 분자 오비탈을 에너지 준위에 따라 나타낸 그림을 '분자 오비탈 에너지 준위 도표(MO diagram)'라 한다. 원자 오비탈을 1s, 2s, 2p, 3s, 3p ... 에너지 순서대로 나열한 도표와 크게 다르지 않다.
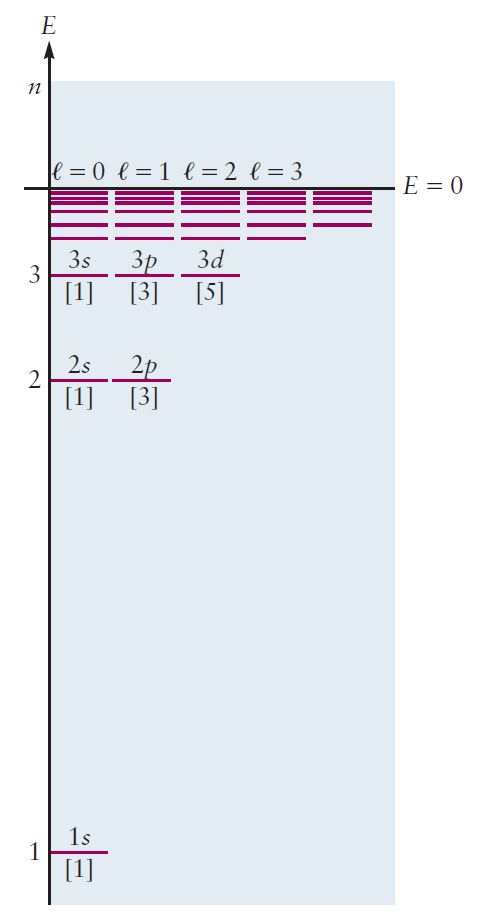

다음은 가장 간단한 분자인 H2의 분자 오비탈 도표를 나타낸 것이다. <그림 4>

분자 오비탈 에너지 준위 도표에는 재료가 된 원자 오비탈(AO)과 분자 오비탈(MO)이 한꺼번에 표현된다. AO는 양 측면에, MO는 중앙에 위치한다.
AO와 MO는 점선으로 연결된다. 점선으로 연결되었다는 것은 해당 MO를 만드는데 관여한 AO라는 뜻이다. 예를 들어 σg,1s 와 σu,1s*는 모두 수소 원자의 1s 오비탈로부터 만들어진 MO이므로, 1s 오비탈과 점선으로 연결된다. 이런 의미에서 분자 상관 도표(correlation diagram)라 불리기도 한다.
2 개의 MO, σg,1s와 σu,1s*의 에너지 준위를 살펴보면, σg,1s는 원자의 1s 오비탈보다 에너지가 낮고, σu,1s*는 에너지가 높다. 원자 오비탈 에너지 도표와 마찬가지로 안정한 오비탈일수록 아래쪽에, 불안정할수록 위쪽에 그려진다.
다전자 원자의 전자 배치 때와 마찬가지로 쌓음 원리(Aufbau principle)에 따라 안정한 오비탈(아래쪽)부터 전자가 채워지며, 파울리의 배타 원리(Pauli's Exclusion Principle)에 따라 한 오비탈에는 최대 2 개의 전자까지 채울 수 있다. 또한 이 글에서는 나오지 않겠지만, 축퇴 상태에 놓인 오비탈에 전자를 채울 때 훈트의 규칙(Hund's Rule) 또한 따른다.
4. 결합 차수(bond order)
결합 세기는 핵 사이 전자 밀도가 얼마나 풍부한가로 판단한다. 핵 사이에 놓인 전자는 양쪽 핵과 동시에 인력 상호작용을 하고, 핵을 일정 거리에 붙잡아둘 수 있다. 두 핵이 전자에 의해 묶이는 꼴이다.
따라서 두 원자 사이에 아무런 상호작용이 없을 때보다 '핵 간 전자 발견 확률이 높다' 또는 '전자 밀도가 증가했다'는 말은 '결합의 형성', '결합 세기의 증가' 등과 연결지을 수 있다.
보강 간섭에 의해 핵 간 전자 밀도가 높아진 결합성 궤도함수(σg,1s)를 전자가 점유할 경우, 분자 전체의 에너지를 낮추는 효과를 갖는다. 반면, 핵간 마디(node)를 갖는 반결합성 궤도함수(σu,1s*)에 전자가 채워질 경우 분자의 에너지는 높아진다. 따라서 안정한 분자를 만들기 위해서는 결합성 궤도함수에 최대한 많은 전자가 채워지고, 동시에 반결합성 궤도함수에 전자가 채워지지 않는 것이 유리하다.
루이스 구조식에서 결합 차수(bond order, B.O)는 선의 개수로 나타난다. 단일 결합은 한 줄(─), 이중 결합은 두 줄(=), 삼중 결합은 세 줄(≡)로 직관적으로 나타낼 수 있다. 그러나 벤젠의 결합 길이는 탄소-탄소 1.5중 결합(결합 차수 = 1.5)에 해당하는 140 pm 이며, 6 개가 모두 동등하다. 단순한 루이스 구조식을 통해서는 이를 설명할 수 없다. 공명(resonance) 개념이 필요하며, 공명 혼성체(resonance hybrid)로 나타내어 실제 벤젠의 구조를 보완해야 한다.
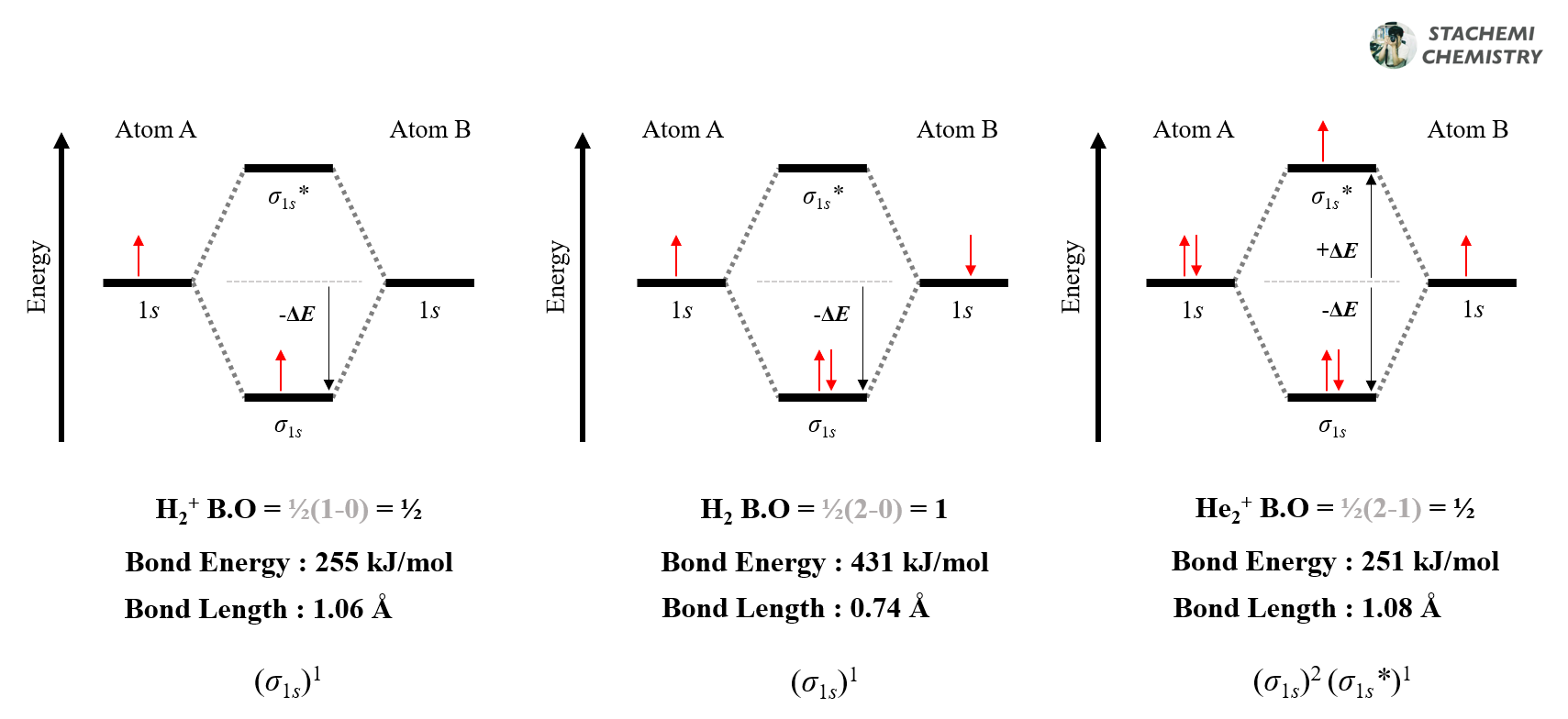
반면, 분자 오비탈 도표에서는 그럴 필요가 없다. 도표에서 나타난 결합성 오비탈에 채워진 전자 수와 반결합성 오비탈에 채워진 전자 수를 통해 간단히 결합 차수를 예측할 수 있다.

<그림 5>의 분자 오비탈 도표를 통해 H2+는 0.5중 결합, H2는 단일 결합, He2+는 0.5중 결합임을 알 수 있다. 결합 차수에 따른 결합 길이, 결합 에너지 차이가 나타남 또한 확인할 수 있다. 결합 차수가 클수록 결합 길이는 짧아지고, 결합 에너지는 커진다.
[참고] 관련 교재 및 단원
- Oxtoby, Principle of Modern Chemistry 7th, Chapter 6. Chemical Bonding and Molecular Structure
LCAO 분자 오비탈
- 끝 -
* 긴 글 읽어주셔서 감사합니다. 내용 중 오타나 문맥상 오류 등이 있는 경우 댓글로 알려주시면, 최대한 빠른 시일 내에 수정/답변드리도록 하겠습니다.
[다음 글] https://stachemi.tistory.com/215
동핵 이원자 분자의 오비탈 (1) σ 오비탈, π 오비탈의 형성
동핵 이원자 분자 오비탈 (1) σ 오비탈, π 오비탈의 형성 0. 들어가기 [연관된 글] 192. 분자 궤도함수 이론 (Molecular Orbital Theory, MOT) 196. LCAO 분자 오비탈 (LCAO MO) 원자 오비탈의 선형조합(LCAO)을 통해
stachemi.tistory.com
'화학 > 화학이야기' 카테고리의 다른 글
| 원자 모형의 변천 (3) 보어의 원자 모형 (4) | 2020.12.18 |
|---|---|
| 수소 선 스펙트럼 (Spectrum of Hydrogen) (4) | 2020.12.12 |
| [스크랩] 용해도 규칙 (Solubility Rule) (0) | 2020.12.01 |
| 분자 궤도함수 이론 (Molecular Orbital Theory, MOT) (2) | 2020.11.27 |
| 반트 호프 식 (van't Hoff equation) - 묽은 용액의 삼투압 (2) | 2020.11.24 |



