* 본문은 다음 글과 연결됩니다.
[이전 글] 215. 동핵 이원자 분자의 오비탈 (1) σ오비탈, π 오비탈의 형성
동핵 이원자 분자의 오비탈 (1) σ 오비탈과 π 오비탈의 형성
동핵 이원자 분자 오비탈 (1) σ 궤도함수와 π 궤도함수의 형성 0. 들어가기 [연관글] 192. 분자 궤도함수 이론 (Molecular Orbital Theory, MOT) 196. LCAO 분자 오비탈 (LCAO MO) 원자 오비탈의 선형조합(LCAO)..
stachemi.tistory.com
동핵 이원자 분자의 오비탈 (2)
N2, O2의 MO 상관 도표
4. N2와 O2 분자 궤도 함수
4.1. 2주기 동핵 이원자 분자의 에너지 준위
2주기 pz 오비탈끼리의 선형조합은 σpz , σ*pz 분자 궤도함수를 만들고, px 또는 py오비탈 간 선형조합은 πpx(y) , π*px(y) 분자 궤도함수를 만든다. 총 6 개의 p-오비탈에 의해 6 개의 분자 궤도함수가 만들어진다.
생성된 분자 궤도함수 에너지 순서는 어떨까?
축 방향 정면 겹침에 의한 σ 궤도함수(pz - pz)가 축을 벗어난 측면 겹침에 의한 π 궤도함수(px(y) + px(y)) 보다 안정화되는 폭이 크지 않을까? 마찬가지로, 반결합성 궤도함수는 σ* 궤도함수(pz + pz)가 π* 궤도함수(px(y) - px(y))에 비해 불안정화되는 폭이 크지 않을까?
<그림 8>의 결과는 우리 예상을 벗어난다.
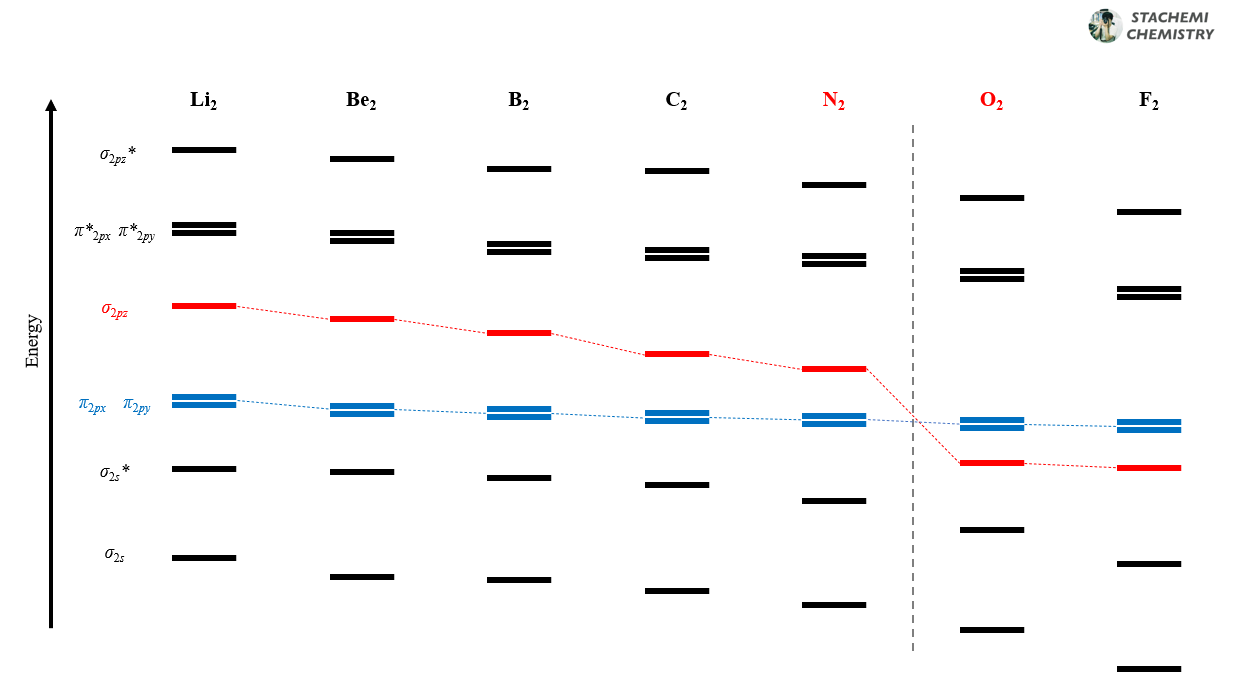
2주기 원소의 동핵 이원자 분자의 에너지 순서를 살펴보면, N2와 O2 사이를 기점으로 달라진다. 결과적으로 Li2, Be2, B2, C2, N2 분자 오비탈의 에너지 순서가 같고, O2, F2, Ne2 분자 오비탈의 에너지 순서가 같다. N2에서 O2로 넘어가면서 σ2pz 오비탈과 π2px(y) 오비탈 순서가 역전된다.
<그림 9>의 N2, O2 분자 오비탈의 순서를 살펴보자.
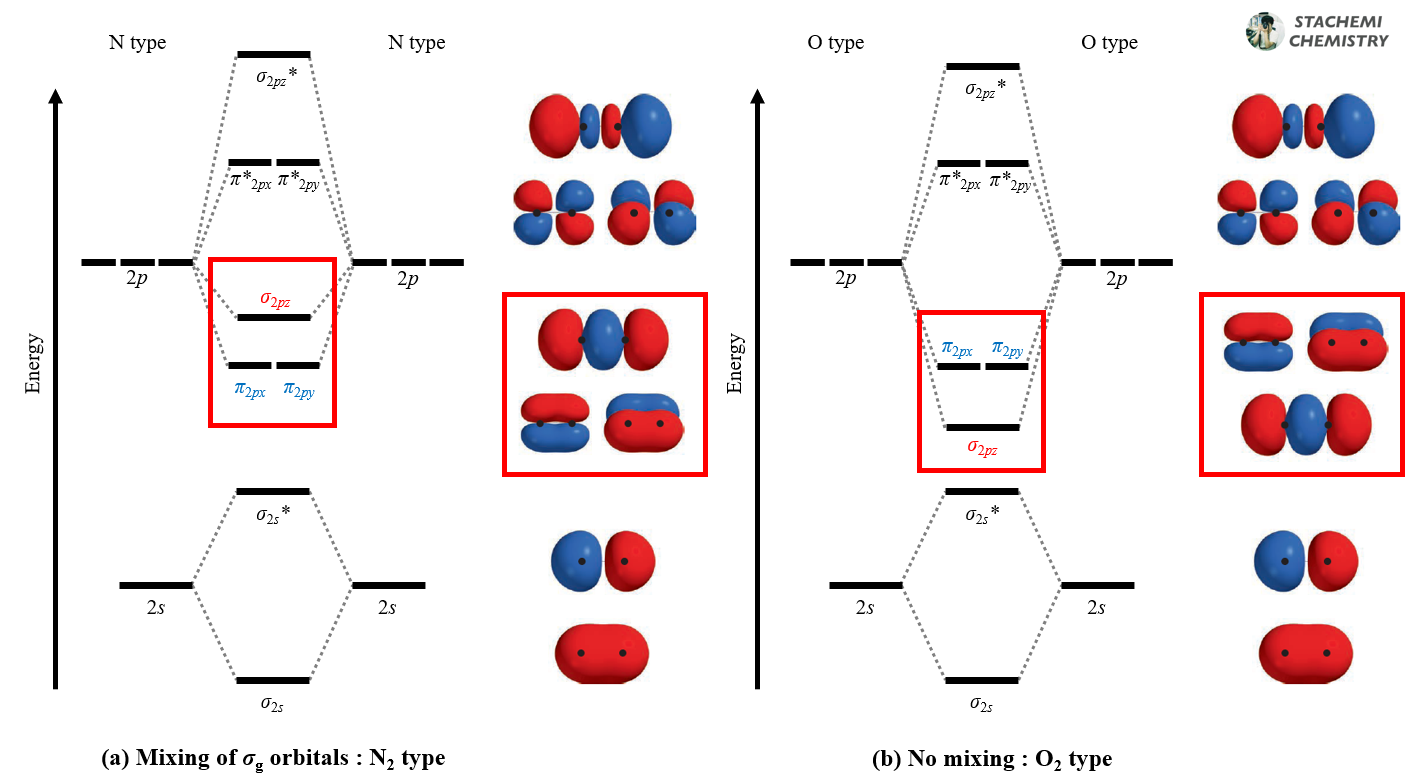
<그림 9-(b)>는 산소(O) 이후 2주기 원자들(O, F, Ne)의 동핵 이원자 분자 상관도표다. 우리가 예상가능한 1-2-2-1(σ-π-π*-σ*) 순서의 일반적인 모습이다. 이를 편의상 O2 타입 상관도표라 하자. (σ2pz < π2px(y))
반면, <그림 9-(a)>는 우리 예상에서 벗어난다. 반결합성 궤도함수인 σ*2pz의 상승 폭(↗↖)에 비해 결합성 궤도함수인 σ2pz의 안정화 폭(↘↙)이 훨씬 작다. 결과적으로는 정면 겹침에 의한 σ2pz 궤도함수 에너지가 측면 겹침의 π2px(y) 궤도함수보다 오히려 높게 자리한다. 마치 원래는 아래쪽에 있어야 할 σ2pz 궤도함수가 무언가에 밀려 위로 올라간듯한 모양새다. (σ2pz > π2px(y))
결과적으로는 밑에서부터 2-1-2-1(π-σ-π*-σ*)의 비대칭적인 에너지 순서를 보인다. 이런 상관 도표를 갖는 대표적인 분자가 N2 이다. 편의상 N2 타입 상관도표라 하자. 질소(N) 이전 2주기 원자들(Li, Be, B, C)의 동핵 이원자 분자는 모두 N2 타입의 순서를 갖는다.
왜 이런 차이(에너지 역전)가 나타나는 것일까?
4.2. 오비탈 에너지의 역전
N2 타입 분자들(Li2 ~ N2)의 에너지 순서가 역전(cross-over)되는 이유를 어떻게 설명할 수 있을까?
한 가지 간단한 설명 방법은 2s 오비탈과 2pz 오비탈이 분자 궤도함수(σ2pz)를 만드는 과정 중에 섞일 수 있다는 점을 고려하는 것이다. 2s 오비탈은 z 축 방향으로 다가오는 2pz 오비탈과 섞일(orbital mixing) 수 있는 대칭성을 갖는다. 앞선 글(215)에서 에너지가 비슷한 2s와 2pz 사이 선형조합이 가능함을 보였었다.
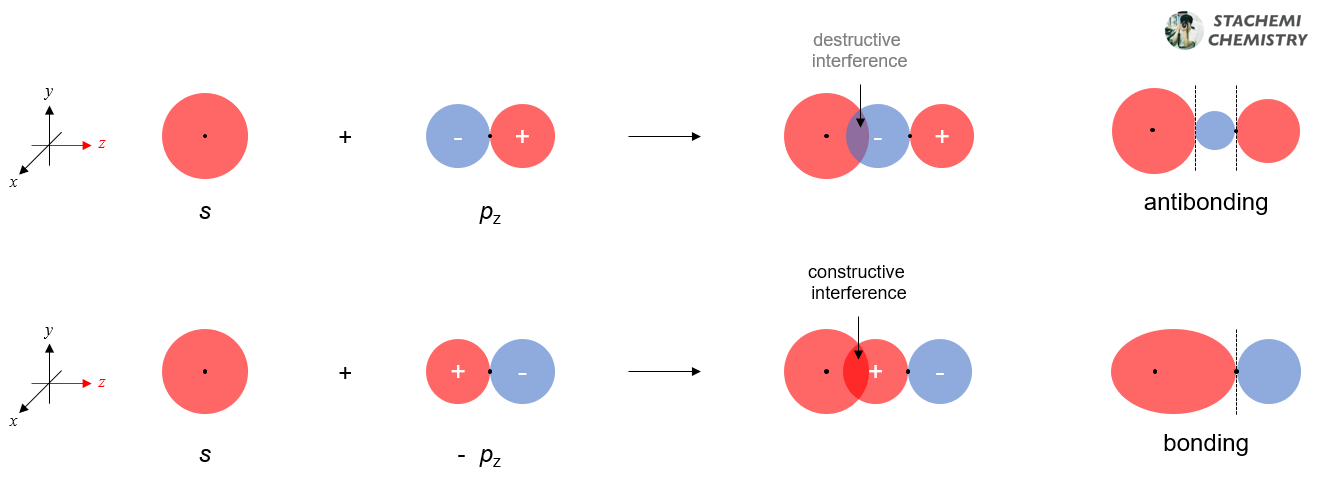
간단히 말해 2pz 오비탈 간 선형조합을 통한 σ2pz 생성 과정에, 2s 오비탈이 영향을 줄 수 있다는 뜻이다. 2s, 2pz 오비탈의 에너지가 유사한 질소(N) 이전까지는 혼합(섞임)이 가능하지만, 두 오비탈(2s, 2pz) 사이 에너지 차이가 큰 산소(O) 원자부터는 혼합이 일어나지 않는 것이다.
2s 오비탈에 의한 영향으로 σ2pz 는 <그림 10-2>와 같이 에너지가 높아지며, 결과적으로 σ2pz 와 π2px(y) 오비탈 사이 역전이 발생하게 되는 것이다.
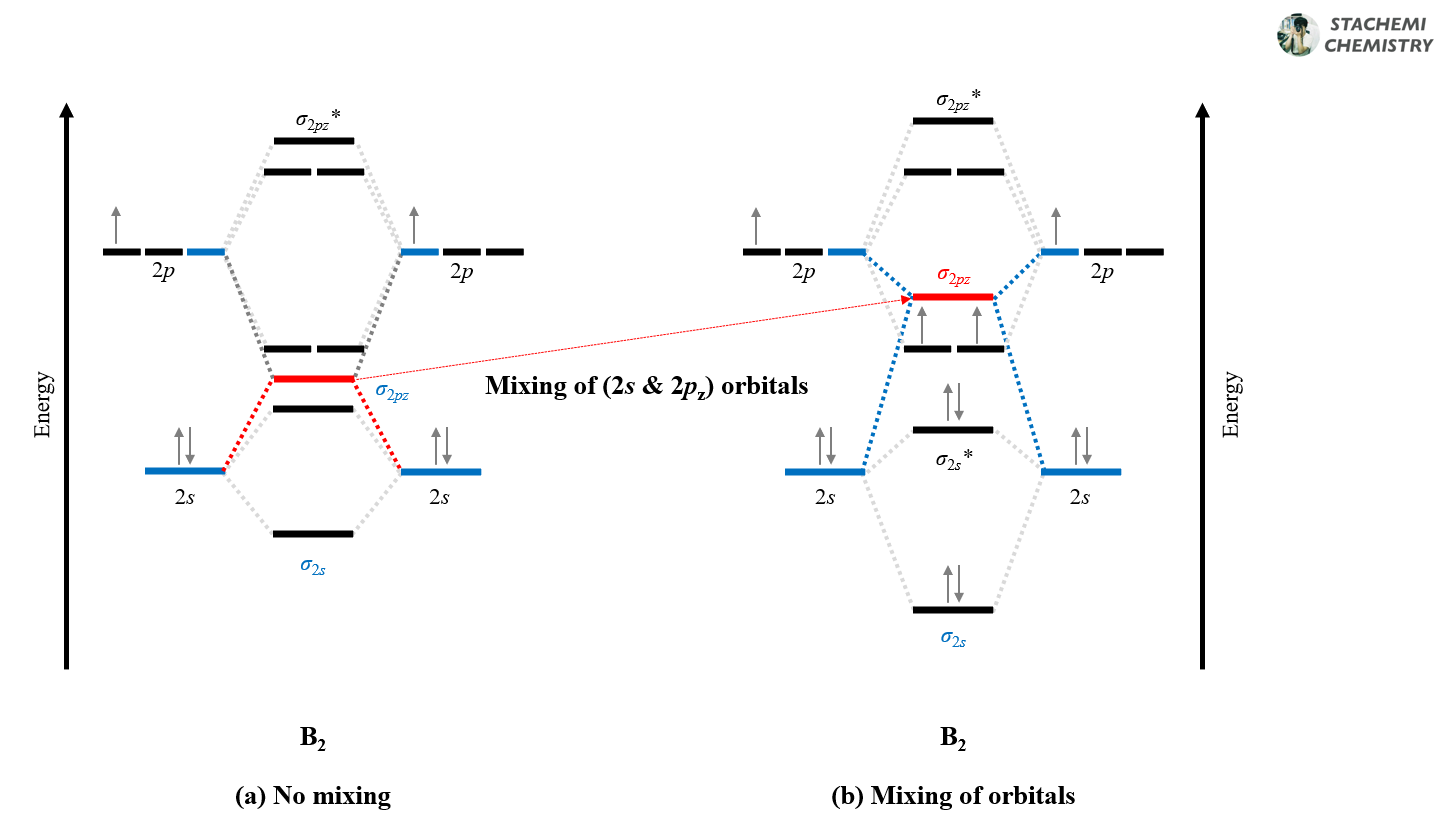
결과는 같겠지만, 다른 방식으로 설명하기도 한다.
먼저, 처음 원자 오비탈(AO)을 통해서 분자 궤도함수(MO)를 만들 때는 에너지 간격에 관계없이 2s와 2pz의 혼합을 고려하지 말자. 2s 오비탈 간 겹침으로 σg,2s, σ*u,2s 궤도함수를 만들고, 2pz 오비탈 간 겹침으로 σg,2pz, σ*u,2pz 궤도함수를 만든다. <그림 10-2, (a)>
그런데, B2, C2, N2 와 같은 분자의 경우 2s와 2p 오비탈에 의해 생성된 σg,2s 궤도함수와 σg,2pz 궤도함수의 에너지가 유사하여 서로 영향을 미칠 수 있게 된다.(혼합, mixing of orbitals)
그 결과 에너지가 낮은 σg,2s는 (혼합에 의해) 보다 안정화(↘)되고, 상대적으로 에너지가 높은 σg,2pz 궤도함수는 (혼합에 의해) 불안정(↗)해진다. 결과적으로 에너지가 높아진 σg,2pz 와 πu,2px(y) 사이 역전이 일어난다. <그림 10-2, 하늘색(a)→(b)>
물론, σ*u,2s와 σ*u,2pz 궤도함수 또한 대칭성 측면에서는 충분히 겹침이 일어날 수 있다. 하지만, 두 오비탈 간 에너지 차이가 상대적으로 커서 혼합에 의한 효과가 극적으로 나타나지 않는다. <그림 10-2, 붉은색(a)→(b)>
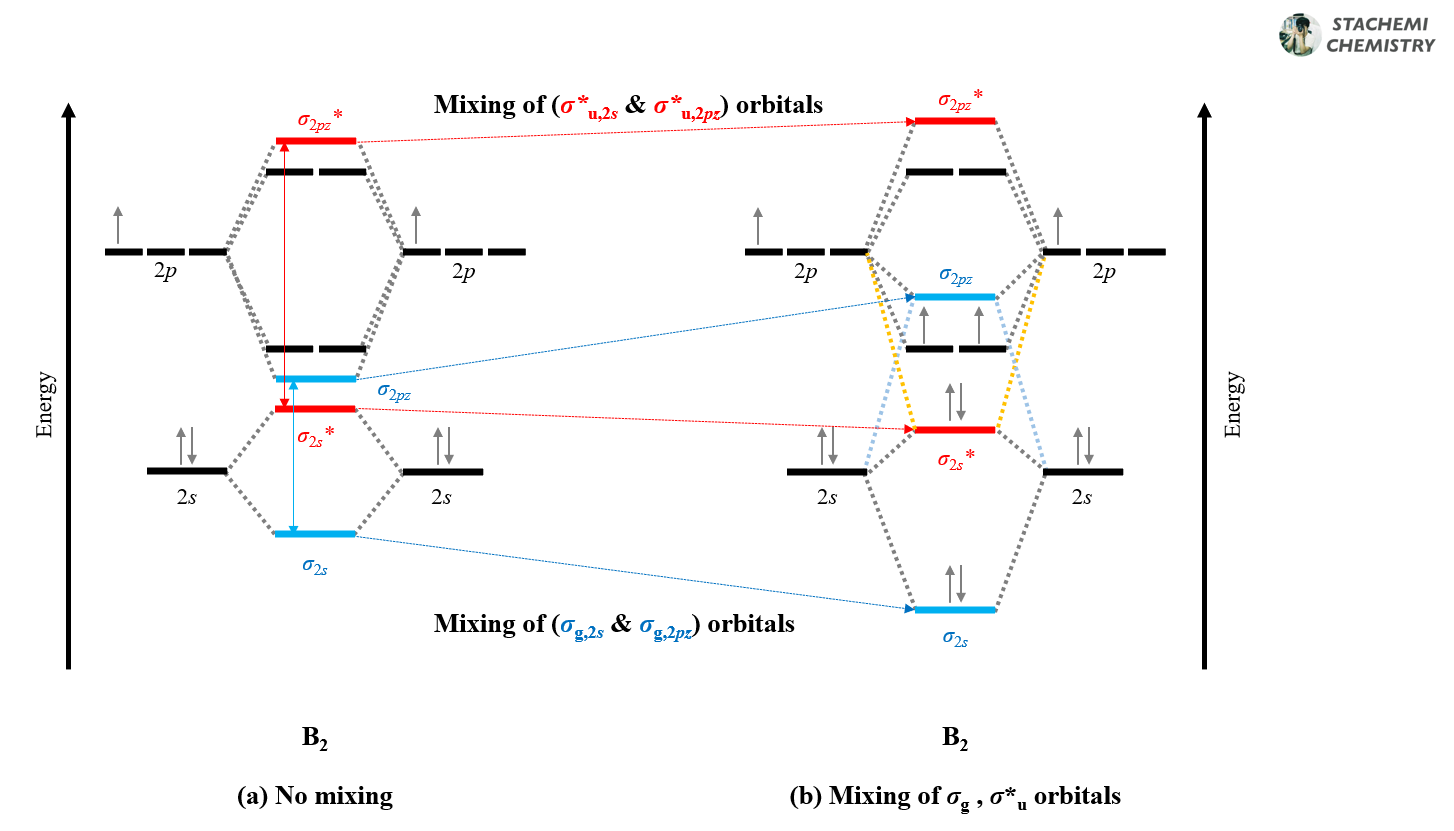
두 설명 방법에 차이가 있지만, 결국에는 혼합을 고려한다는 점에서 같다. 앞선 설명은 원자 오비탈 간의 혼합<그림 10-1>을 통해, 뒤의 설명은 생성된 분자 오비탈 간의 혼합<그림 10-2>을 통해 에너지 역전을 설명한다. 언제 혼합을 따져주는가의 차이일 뿐이다.
분자 오비탈 혼합에 의한 에너지 역전은 B2와 C2 분자의 자기적 성질에 영향을 준다. 만약 오비탈 혼합이 고려되지 않는다면, B2 분자는 반자성, C2 분자는 상자성으로 예측되지만, 실제 B2 분자는 상자성, C2 분자는 반자성을 나타낸다.
4.3. 분자 오비탈 상관도표의 해석 (N2 vs O2)
분자 오비탈 상관도표는 우리에게 다양한 정보를 준다.

4.3.1. 결합 차수 (Bond Order)
분자 오비탈 상관도표를 통해서 결합차수를 확인할 수 있음을 이전 글을 통해 알아보았다. 다음 <그림 11-1>를 통해 N2는 결합차수가 3, O2의 결합차수가 2임을 알 수 있다.
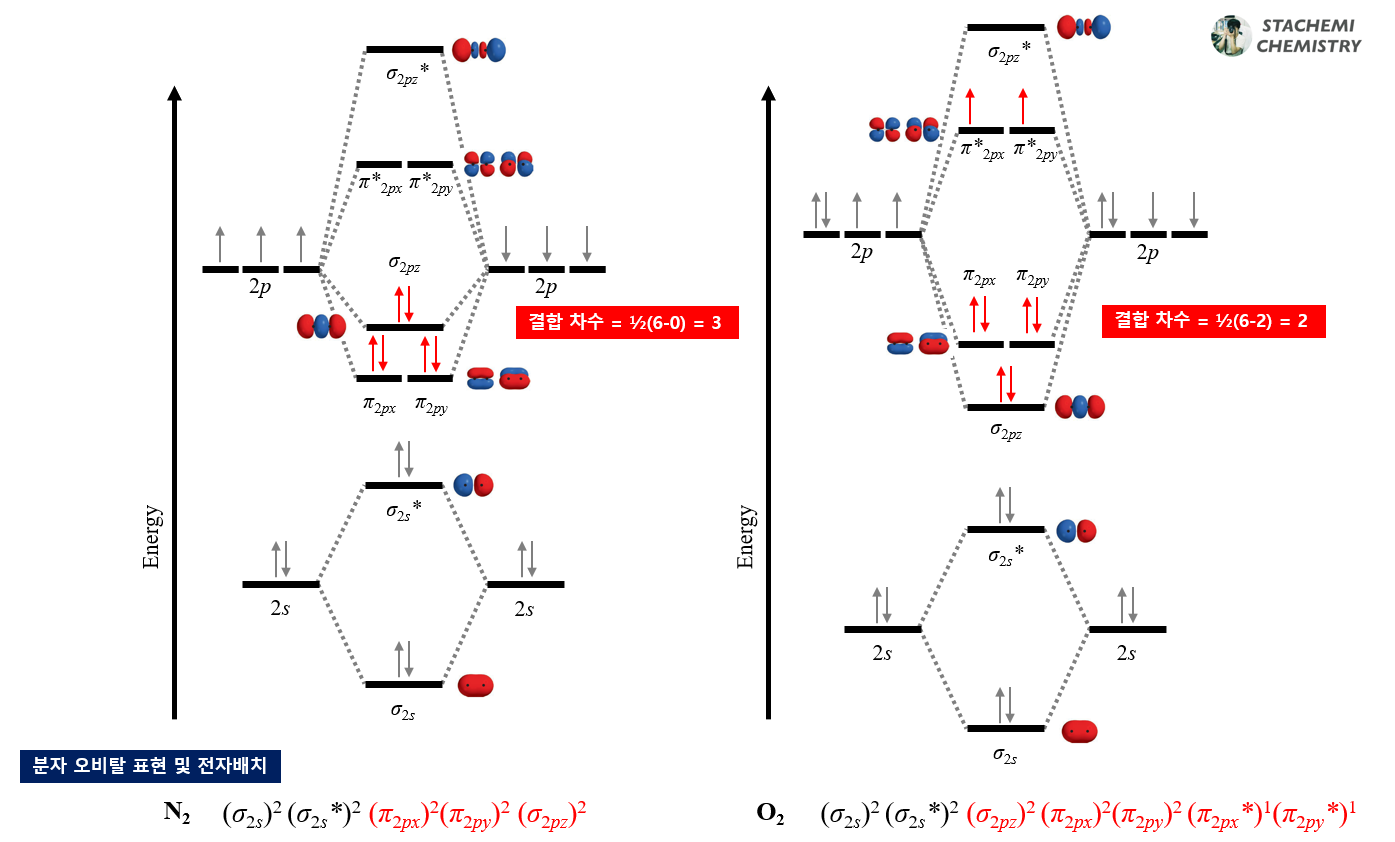
4.3.2. HOMO, LUMO
분자의 전자배치를 통해 HOMO와 LUMO를 알 수 있다. HOMO는 Highest Occupied Molecular Orbital의 약자로, 전자가 채워진 가장 높은 분자 오비탈을 가리킨다. LUMO는 Lowest Unoccupied Molecular Orbital의 약자로, 전자가 채워지지 않은 가장 낮은 분자 오비탈을 말한다.
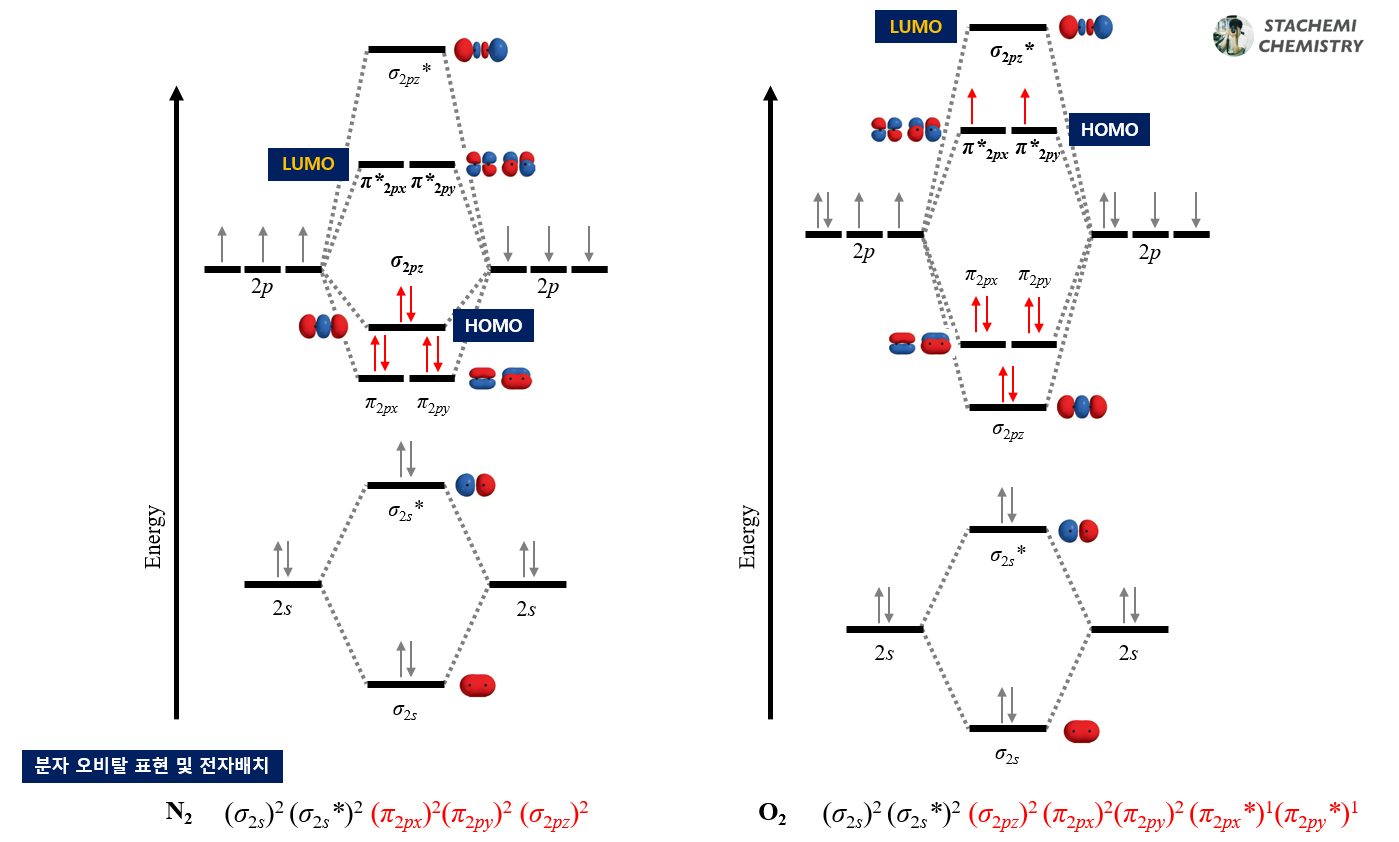
N2의 HOMO는 σ2pz 오비탈이며, O2의 HOMO는 π*2px, π*2py 오비탈이다. 또한 N2의 LUMO는 π*2px, π*2py 오비탈, O2의 LUMO는 σ*2pz 오비탈이다.
4.3.3. 자기적 성질 (magnetic property)
분자 궤도함수의 상관도표는 분자의 자기적 성질을 예측, 설명하는데 유용하게 사용될 수 있다. O2는 상자성(paramagnetic property)을 띠지만, 루이스 구조식을 바탕으로 하는 원자가 결합 이론을 통해서는 설명이 어렵다. O2의 루이스 구조식에는 홀전자가 나타나지 않는다.
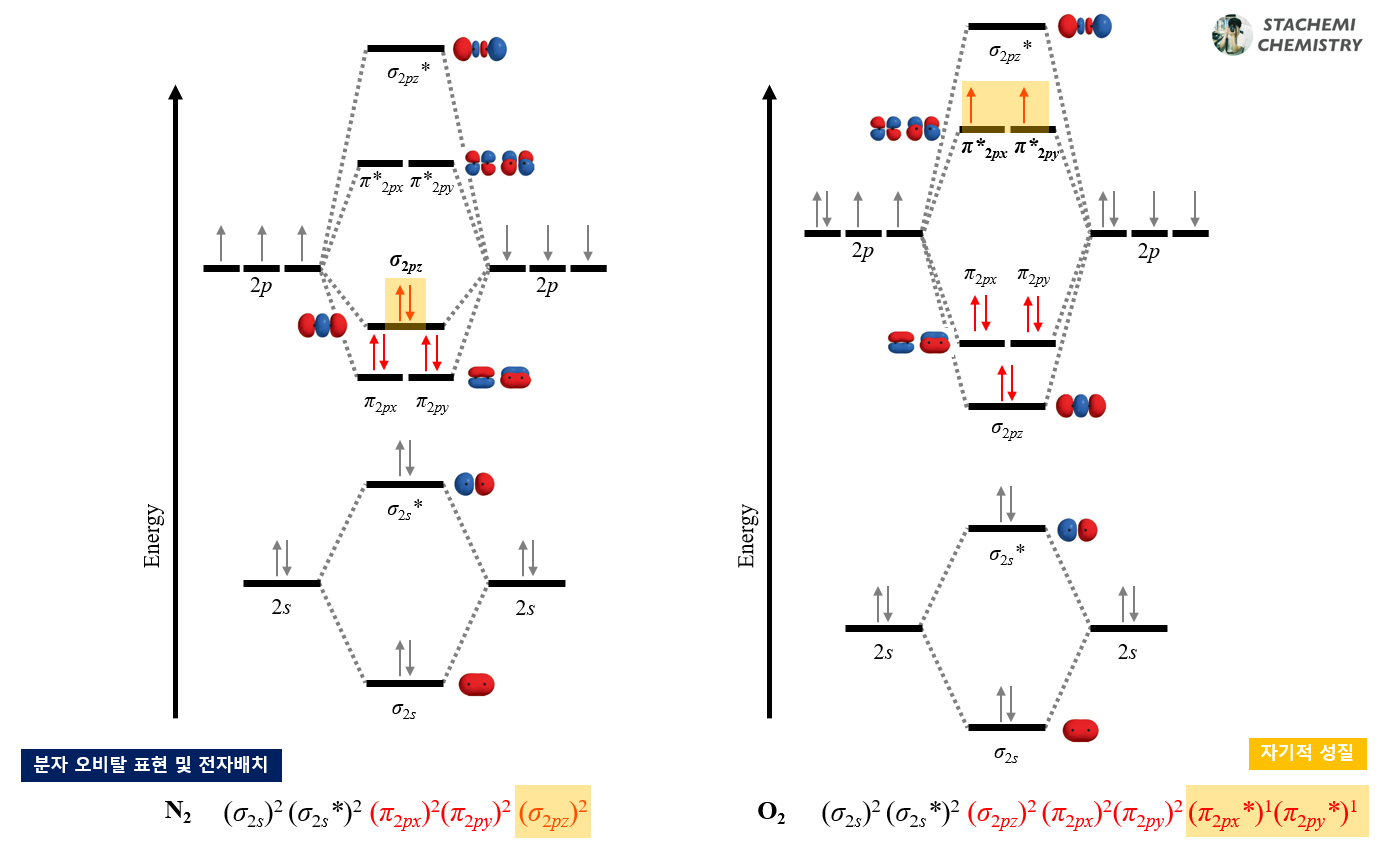
그러나 O2의 분자 오비탈을 통한 전자배치와 상관도표를 보면, π*2px, π*2py 오비탈에 홀전자를 갖는다는 사실을 직관적으로 알 수 있다. 반대로 N2는 전자 배치상 홀전자를 갖지 않으며, 반자성(diamagnetic property)을 가질 것이라 예측할 수 있다. 분자의 자기적 성질을 예측, 설명하기 위해서는 분자 궤도함수 이론이 필요하다.

4.3.4. 원자와 분자의 이온화 에너지
원자의 이온화 에너지는 중성 원자 1몰로부터 전자 1몰을 떼어내어 1가 양이온을 만드는데 필요한 에너지의 크기를 말한다. 즉, 전자의 에너지(오비탈의 에너지 준위)가 낮을수록 떼어내는데 많은 에너지가 필요하다.
N + Ionization Energy → N+ + e-
O + Ionization Energy → O+ + e-
분자의 이온화 에너지는 중성 분자 1몰로부터 전자 1몰을 떼어내어 1가 양이온 분자를 만드는데 필요한 에너지의 크기라 할 수 있겠다. N2 분자 1몰을 N2+ 이온 분자 1몰로 만들기 위해 필요한 에너지라 할 수 있다.
N2 + Ionization Energy → N2+ + e-
O2 + Ionization Energy → O2+ + e-
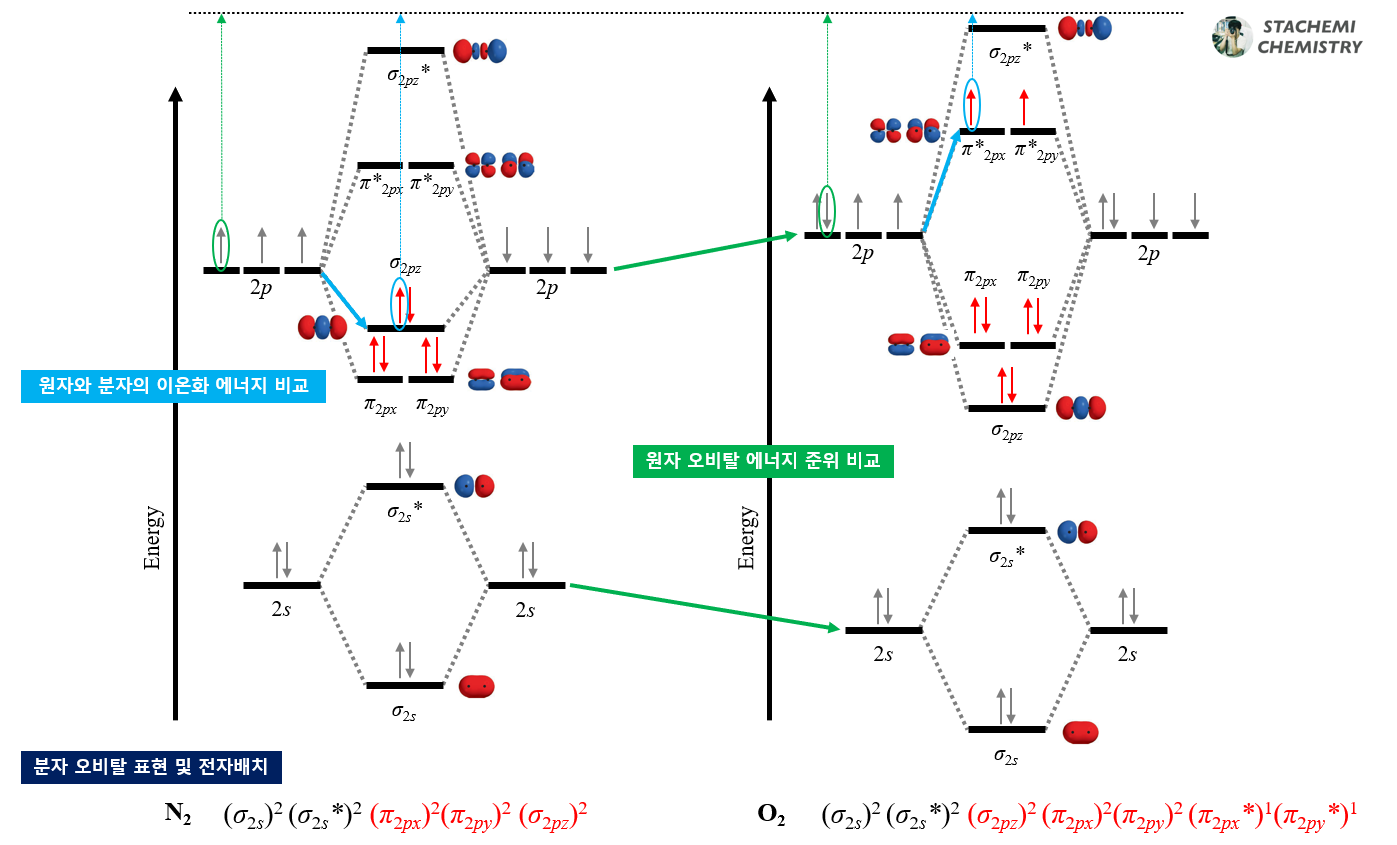
최소한의 에너지를 가하여 분자를 이온화시키기 위해서는 HOMO 준위의 전자를 떼어내는 것이 유리하다. 즉, 원자와 분자의 이온화 에너지 비교는 원자가 전자의 에너지 준위와 분자의 HOMO 에너지 준위의 비교라 할 수 있다.
질소 분자(N2)는 질소 원자(N) 2p 오비탈보다 낮은 HOMO (σ2pz)를 갖는다. 따라서 질소 분자(N2)가 질소 원자(N)보다 이온화 에너지가 크다. (전자를 떼어내기 어렵다.)
분자 N2 이온화 에너지(15.58 eV) > 원자 N 이온화 에너지(14.53 eV)
반대로 산소 분자(O2)의 HOMO는 반결합성 궤도함수인 π*2px(y)이며, 산소 원자(O)의 2p 오비탈보다 불안정하다. 따라서 산소 분자(O2)가 산소 원자(O)보다 이온화 에너지가 작다. (전자를 떼어내기 쉽다.)
분자 O2 이온화 에너지(12.03 eV) < 원자 O 이온화 에너지(13.62 eV)
5. 광전자 분광법 (Photoelectron Spectroscopy, PES)
분자 궤도함수 이론(MO Theory)은 원자가 결합 이론(VB Theory)에 비해 다소 직관성이 떨어지고 어려워보이지만, 상관도표를 해석할 수 있다면, 많은 정보를 한꺼번에 얻을 수 있기에 매우 유용하다. 2주기 동핵 이원자 분자의 경우 질소와 산소를 기점으로 오비탈 에너지 준위의 역전이 일어난다는 것 또한 상관도표를 통해 확인할 수 있다.
그렇다면, 실제 분자의 에너지 준위 순서는 어떤 방법을 통해 알아냈을까? 분자의 결합 길이를 비롯한 에너지 준위 측정 등은 광전자 분광법(Photoelectron Spectroscopy) 등을 통해 이루어진다.
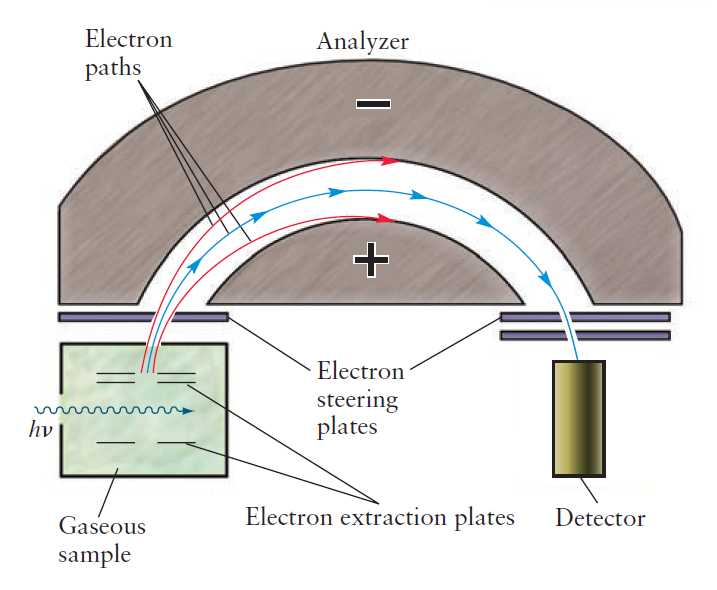
광전자 분광법은 가스 상태의 분자에 X-선을 쬐어주어 최외각의 전자를 제거한다. 이후 방출된 전자의 운동 에너지를 측정하여 이온화 에너지를 측정한다. 초기 가해준 에너지의 크기에서 방출된 전자의 운동에너지를 빼면, 분자에서 전자를 떼어내는데 소요된 에너지의 크기를 알 수 있다. 그리고, 그렇게 구한 이온화 에너지는 Koopmans 근사를 전제하여 떨어져 나온 전자가 속해있던 오비탈의 에너지 준위로 판단할 수 있다.
분자의 이온화 에너지 = 쏴 준 광자(X-선)의 에너지(hυ) - 방출된 전자의 운동 에너지(½mv^2)

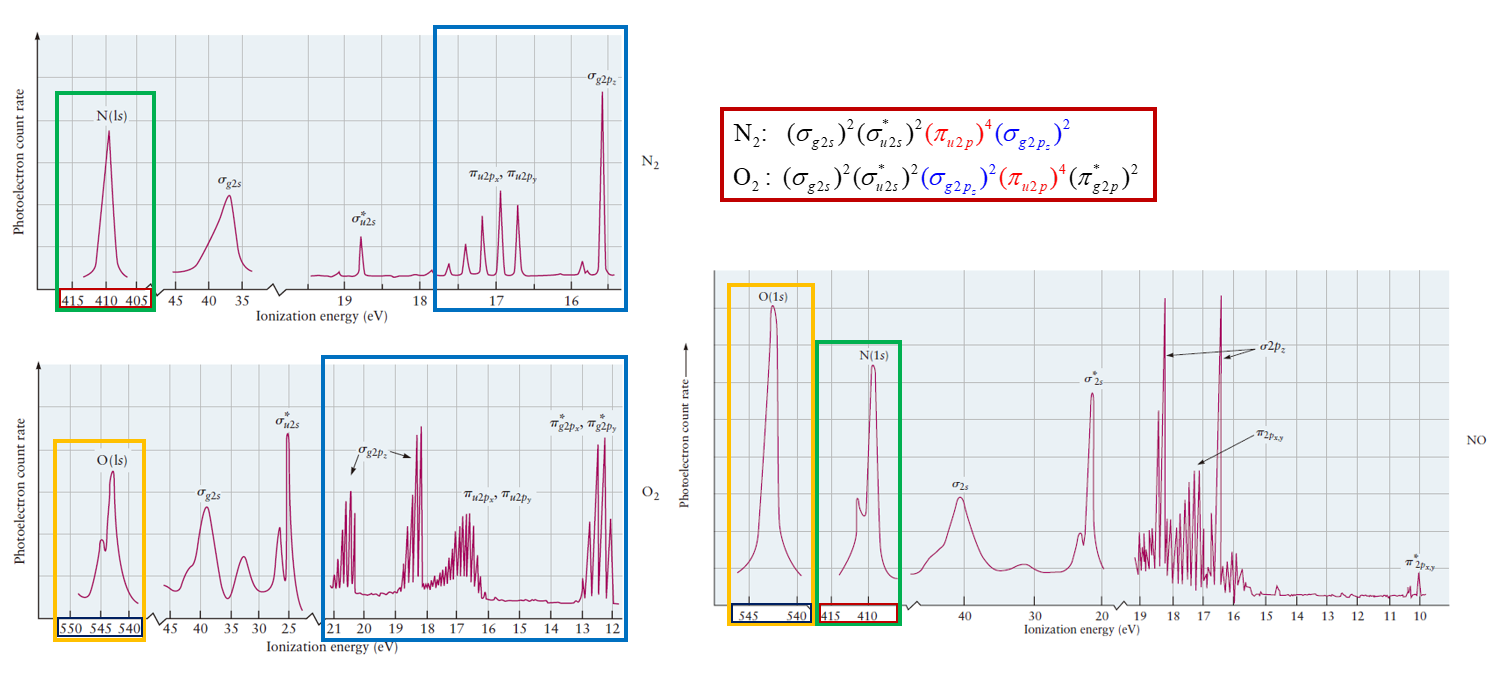
위의 <그림 14>의 N2, O2, NO 분자의 PES 스펙트럼에 나타난 내부 전자(N1s, O1s)의 경우 서로 다른 분자를 형성했음에도 떼어내는데 필요한 에너지 값이 거의 같았다. (N1s = 410 eV, O1s = 542.5 eV)
이는 내부 전자들은 화학 결합 과정에 별달리 관여하지 않으며, 결합에 대한 분자 궤도함수 분석에서 무시될 수 있다는 사실을 명확하게 보여주는 것이다.
동핵 이원자 분자의 오비탈 (2)
- 끝 -
* 긴 글 읽어주셔서 감사합니다. 내용 중 오타나 오류 등이 있는 경우 댓글로 알려주시면, 최대한 빠른 시일 내에 수정/답변드리도록 하겠습니다.
'화학 > 화학이야기' 카테고리의 다른 글
| [스크랩] 원자의 구조 읽기 자료 (0) | 2021.05.10 |
|---|---|
| 원자가와 원자가 전자 (valence & valence electron) (4) | 2021.04.30 |
| 동핵 이원자 분자의 오비탈 (1) σ 오비탈, π 오비탈의 형성 (4) | 2021.02.15 |
| 이온 반지름 비를 통한 결정 구조 예측 (2) | 2021.02.01 |
| 여러 가지 단위 환산 (2) | 2021.01.29 |



