1. 투광도와 흡광도
투광도(transmittance, T )는 빛이 얼마나 시료를 잘 통과하는가에 대한 척도이며, 흡광도(absorbance, A )는 시료가 얼마나 빛을 잘 흡수하는가를 나타내는 척도이다. 투광도가 클수록 시료의 흡광도는 작아지며, 빛을 잘 흡수하는 물질일수록 빛이 잘 투과하지 못한다.
이렇게 의미적으로만 보면 마치 투광도와 흡광도가 서로 자유롭게 변환될 수 있는 개념처럼 보이지만, 실제로 두 개념을 상호 전환하기 위해서는 로그 관계를 거쳐야 한다.

다시 말해, 투광도 0.1은 시료가 초기 빛의 10 %를 투과시켰다는 의미이지만, 그렇다고 곧 흡광도가 0.9인 것은 아니다. 이 경우 흡광도는 1이다. 마찬가지로 투광도 0.01은 1 %의 빛을 투과시켰다는 의미이지만, 흡광도는 0.99가 아닌, 2이다.

투광도는 쪼여주는 빛(P0 )과 시료를 통과한 빛(P )의 비율(P / P0)로 정의되기에, 철저히 시료 통과 전후의 빛의 세기 값의 차이에 의존하여 결정되는 값이다. 반면, 흡광도는 시료의 농도(c ), 빛이 거치는 거리(b ) 등에 영향 받으며, 이 관계를 정리해놓은 것이 비어-람베르트 법칙(Beer-Lambert's Law)이다.

2. 투광도와 농도 사이의 로그 관계가 성립하는 이유
흡광도(A )는 시료의 농도(c )에 선형적으로 비례한다. 이를 비어 법칙(Beer's Law)이라 한다. 따라서 투광도(T )와 농도(c ) 사이에 로그 관계가 성립함을 보인다면, 자연스럽게 선형 비례 관계에 놓인 흡광도 또한 투광도와 로그 관계가 성립함을 보일 수 있다.
한 번 알아보자.

세기가 P0 인 빛이 N [개]의 시료 입자를 포함한 용액을 통과하며, 빛이 통과하는 길이가 b [cm]라고 하자. 빛이 통과하면서 시료 입자들에 의해 흡수되기 때문에 빠져나온 빛의 세기는 P 로 감소한다. (P0 > P )
단면적이 S 이고, 두께가 dx [cm]인 미소한 용액 구역을 빛이 통과한다고 생각해보자. 이 구역에는 dN [개]의 시료 입자들이 있다. 이 시료 입자들에 의해 직접적인 광자의 흡수가 일어나는 면적은 단면적 S 에 비해 매우 미소한 면적을 차지할 것이기에 미소 면적 dS [cm2]라 표현할 수 있다.
흡광 과정을 통계적 평균으로 이해해보면, 전체 단면적(S ) 중 시료 입자가 차지하고 있는 면적(dS )의 비율(dS /S )만큼 빛의 세기의 변화( - dPx / Px )가 나타날 것이다.
음의 부호는 빛의 세기가 감소함을 뜻한다. 빛의 세기 감소 비율과 면적 비율에 관한 관계식은 다음과 같이 나타낼 수 있다. 식 (1)
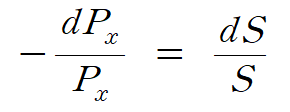
여기서 빛의 세기 Px 는 단위 시간 [초]당 단위 면적 [cm2]에 들어온 광자(빛 알갱이) 수에 비례한다. 약해지는 빛의 세기 dPx 역시 단위 시간 [초]당 없어지는 광자 수라 할 수 있다.
dS [cm2]는 시료 입자 dN [개]이 차지하는 면적의 합이고, 결국 이 값은 이 구역 내에 존재하는 입자수 dN [개]에 비례한다는 것을 알 수 있다. 비례 상수를 통해 식을 나타내면 다음과 같다. 식 (2)

위의 (1), (2)식을 조합하여, 이를 적분하면 다음과 같다. 식 (3)
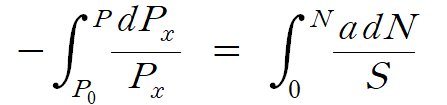
적분 한계는 N = 0 일 때, P = P0 (초기 입사광의 세기)가 되며, N = N 일 때, P = P (빠져나온 빛의 세기)가 된다. 좌변의 (1/x) dx 적분은 lnx 형태로 변환되며, 위 (3)식은 다음과 같이 정리된다. 식 (4)
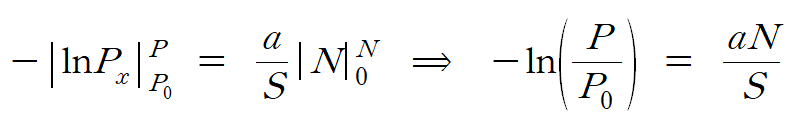
자연로그(ln)와 상용로그(log) 관계 lnz = (ln10)(logz) = 2.303logz 를 이용하여 변환해주면 다음 식을 얻을 수 있다. 식 (5)

용액의 부피 V [cm3] = 단면적 S [cm2] * 셀의 길이 b [cm]으로 나타낼 수 있기 때문에 S [cm2] = V / b 로 변환 가능하다.
또한 입자의 개수 N [개]은 아보가드로 수 NA [개/mol]를 이용하면, 용액 내 포함된 시료 입자의 몰수 n [mol]으로 변환 가능하다. (N [개] = n [mol] * NA [개/mol]) 식 (6)
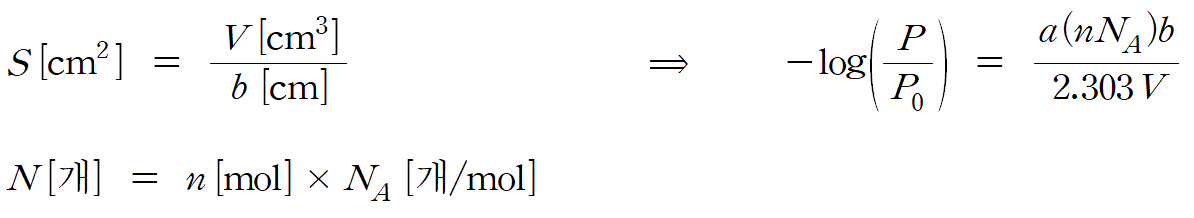
부피 V [cm3]를 리터 단위[L]로 바꿔주기 위해 1000 [cm3] = 1 [L]의 등가식을 이용하면, 최종적으로 n /V 를 몰농도 c [mol/L ]로 변환할 수 있게 된다. 최종식의 형태는 다음과 같다. 식 (7)

결국 투광도(T )와 몰농도(c ) 사이에 로그 관계가 성립함을 보임으로써 흡광도(A )와 투광도 역시 로그 관계를 통해 변환될 수 있음을 보였다. 이는 용액을 통과하는 과정에서, 빛의 세기 감소가 시료의 두께(통과 길이, b)와 몰농도(c )에 따라 지수함수적으로 감소한다는 것을 뜻한다.
[참고한 글]
- Skoog, Fundamentals of Analytical Chemistry, 9th, 660~662p, Feature 24-2 Deriving Beer's Law
3. 덧붙여
해리스 분석화학, 9판, 479p의 <보충 18-1>의 설명은 Skoog에서 제시된 유도 과정과 거의 유사하지만, 보다 간단한 편이다. 경우에 따라서는 이 증명 과정이 더 이해하기 쉬울 수 있겠다.

빛의 세기가 P 인 빛이 두께가 dx 인 미소하게 얇은 용액 층을 통과한다고 생각해보자.
흡광 과정을 물리적 모형에 의하면, 빛이 매우 얇은 dx 층을 통과하면서 초기 빛의 세기보다 미소하게 감소할 것이다. dx 층을 통과하는 과정에서의 미소한 빛 감소량은 dP 라고 표현할 수 있다.
빛 감소량은 얇은 층을 통과할 때의 빛의 세기 P 와 용액의 농도 c , 그리고 빛이 통과하는 용액층의 두께인 dx 에 비례한다. 또한, 빛의 세기는 용액을 통과할수록 감소하므로 음의 부호가 붙어야 함을 알 수 있다. 이를 적당한 비례상수 β 를 도입하여 등식을 세워주면 다음과 같이 표현된다.
* 1000개의 입사된 빛(광자) 중에 1개의 광자가 용액의 얇은 층에 의해 흡수된다면, 2000개의 입사 빛(광자) 중에는 2개가 흡수될 것으로 예상 가능하다. 즉, 광자 수(빛의 세기)의 감소는 단위 시간당 단위 면적을 지나가는 광자의 수, 즉 광자의 입사 선속(flux)에 비례한다.
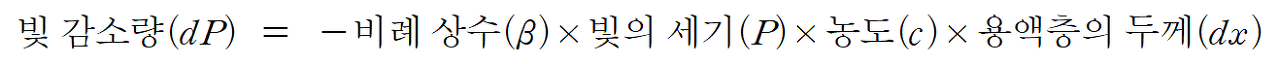
위 식을 재배열하여 적분하면, 시료를 통과하는 빛의 세기를 구할 수 있다. 위 모형에 따라 적분 한계는 x = 0 일 때, P = P0 (초기 입사광의 세기)가 되며, x = b 일 때, P = P (빠져나온 빛의 세기) 가 된다.
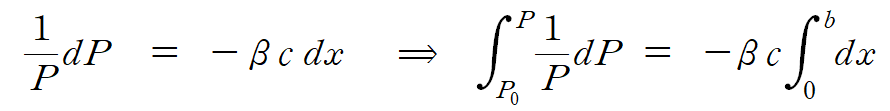
(1/x)dx에 대한 적분은 lnx 형태로 변환된다. 따라서 위 식은 다음과 같이 정리된다.

마지막으로 자연로그(ln)와 상용로그(log) 관계 lnz = (ln10)(logz)를 이용하여 변환해주면 다음 결과식을 얻을 수 있다.

농도(c )와 투광도(T ) 사이의 로그 관계는 빛이 용액의 미소한 얇은 층을 통과하는 과정에서 감소하고, 그 감소 정도가 입사광의 세기(P )에 비례한다는 사실로부터 유도된다. 빛은 시료 층을 통과하는 동안 연속적으로 세기가 감소하기 때문에, 각 층에서의 세기 감소는 점차 줄어든다.
'화학 > 화학이야기' 카테고리의 다른 글
| 자유에너지와 화학 평형의 위치 (46) | 2020.08.22 |
|---|---|
| 아레니우스에 대한 모든 것 (4) | 2020.08.16 |
| 원자 모형의 변천 (2) 원자핵의 발견 (6) | 2020.07.28 |
| 지레 규칙 (Lever Rule) (0) | 2020.07.23 |
| 고등학생을 위한 분광광도법 : (3) 정량분석 (8) | 2020.07.17 |



