0. 들어가기
모든 문항을 모두 풀어 정리해두기에는 시간이 너무 지날 것 같아서 3점 문항만 풀이를 해둔다. 요즘 시간을 끌기 위해, 적은 정보만 주고, 이리저리 꼬아댔던 경향에 비하여 3점 문항은 전체적으로 쉽게 출제되었던 것 같은 느낌이 있다. 하지만, 오히려 비킬러 2점 문항 중에 시간이 걸렸을 것 같아 보이는 문제가 몇몇 보이니, 학생들이 느끼는 체감 난이도는 비슷했을 것 같다. 여전히 수능 화학에 대해서는 마음에 드는 부분도, 마음에 들지 않는 부분도 함께 있다.
메디컬 계열을 희망하거나 인서울권 이공계 학과를 희망하는 학생들 외의 관심을 받기 점점 어려워지는 것 같아 안타깝다. 교실에는 메디컬 계열과 인서울권 이공계 학과를 진학하는 학생 비율이 그렇지 않은 학생들보다 적다. 개인적으로는 그저 화학을 좋아하는 학생들이 수능 화학을 선택할 수 있도록 이끄는 문제가 출제되었으면 좋겠다.
2024학년도 수능 6월 모의평가(2023.6.1.) 화학1 3점 문항 풀이
3번, 4번, 6번, 8번, 12번, 13번, 14번, 17번, 19번, 20번

[3번 답] ④ ㄴ, ㄷ
[풀이]
반응 전후의 알짜 변화를 반응식으로 나타내면 다음과 같다.
2XY + Y2 → 2XY2
ㄱ. 전체 분자 수는 반응 전 5 분자에서 반응 후 4 분자로 감소한다. (거짓)
ㄴ. 생성물의 종류는 XY2 1가지이다. (참)
ㄷ. 반응 후 4 mol의 XY2가 생성된다면, 반응한 Y2의 몰수는 2 mol 이다. (참)

[4번 답] ⑤ HCl, CF4
[풀이]
탐구 과정의 결과와 결론이 타당하다는 뜻은 초기 설정한 가설에 대한 올바른 과정을 거쳤으며, 해당 과정으로부터 얻은 결과로부터 옳은 결론을 내렸다는 말이다. 즉,
극성 공유 결합을 갖는 분자들의 분자 극성 여부를 확인한 결과를 통해, 스스로 초기 설정한 가설의 옳고 그름을 판단할 수 있다는 뜻이다.
학생은 "극성 공유 결합이 있는 분자는 모두 극성 분자이다."라는 가설을 최종적으로 받아들이지 않았으며, 이는 탐구 과정 및 결과로부터 기인하였기에 결과 표의 ㄱ, ㄴ의 예시는 극성 공유 결합을 갖지만, 분자의 극성이 극성(ㄱ)인 예와 무극성(ㄴ)인 예가 되어야 한다.
따라서 (ㄱ) HCl, (ㄴ) CF4가 적합하다. 참고로, O2는 무극성 공유 결합 + 무극성 분자, HCl은 극성 공유 결합 + 극성 분자, CF4는 극성 공유 결합 + 무극성 분자의 예시가 될 수 있다.

[6번 답] ④ ㄴ, ㄷ
[풀이]
W, X, Y, Z에 해당하는 원소를 가려내기에 가장 적합한 분자는 YZ3 이며, NF3 분자로 예측 가능하다. C, N, O, F 중 질소는 3의 결합 원자가를 가지며 최대 3개의 결합을 갖기 때문에, Y = 질소(N), Z = 플루오린(F)로 예상할 수 있다.
구성 원자의 원자가 전자 수 합을 살펴보아도 질소(= 5) + 플루오린(= 7*3) = 26으로 타당하다.
ㄱ. WX2에 이중 결합이 존재한다면, W의 결합 원자가는 4로 탄소(C), 만약 단일 결합만 존재한다면 결합 원자가는 2로 산소(O)를 예상할 수 있지만, X가 플루오린이 될 수 없기 때문에 W = 탄소(C), X = 산소(O)로 예상할 수 있다. 분자 WZ2는 CO2 이다. (거짓)
ㄴ. W, X, Y, Z 이 모두 밝혀졌기 때문에, YWZ 는 FCN 임을 알 수 있다. FCN 분자에는 F에 비공유 전자쌍 3쌍,N에 비공유 전자쌍 1쌍으로, 총 4쌍을 갖는다. (참)
ㄷ. 구성 원자의 원자가 전자 수 합 (ㄱ) = 탄소(= 4) + 산소(= 6*2) = 16 이다. (참)
[8번 답] ① ㄱ
[풀이]
X와 Y의 오비탈 전자수 비가 같다. 바닥 상태 전자 배치에서 1s, 2s 오비탈이 완전히 채워지지 않은채로 2p 오비탈에 전자가 채워지는 경우는 없다. 따라서 최소 2주기 원소의 경우 s 오비탈에 채워진 전자수는 4이고, p 오비탈에 채워진 전자수는 1 ~ 6까지의 값을 갖는다.
표의 (ㄱ)이 p 오비탈이라면, 바닥 상태 전자 배치로 X, Y 원자의 2/3 = 4/6 = 6/9의 값을 가질 수 없다. 따라서 표의 (ㄱ)은 s-오비탈이라고 할 수 있다. (Z의 3/5 = 6/10 또한 가질 수 없다.)
X와 Y는 2/3으로 표현되어 있지만, 2주기 원소의 바닥 상태 전자 배치상으로는 4/6이어야 한다. 1s와 2s 오비탈에 4개, 2p 오비탈에 6개의 전자가 순서대로 채워진 원자는 네온(Ne)이 되겠다.
또한 3주기 원소라면, 6/9도 가능하다. 1s, 2s, 3s 오비탈에 순서대로 6개, 2p와 3p 오비탈에 6+3 = 9개가 채워진 경우 2/3 비를 만족한다. 이 경우는 인(P)이 된다.
제시문에서 Y의 원자번호가 X보다 크다고 했으므로, X = 네온(Ne), Y = 인(P) 이다.
마지막으로 Z의 3/5 = 6/10으로 바꾸어 생각할 수 있으며, 1s, 2s, 3s 오비탈에 2+2+2 = 6개 전자가 채워지고, 2p에 6개, 3p 오비탈에 4개 전자가 채워진 황(S)임을 알 수 있다. Z = 황(S)
ㄱ. 2주기 원소는 네온(X) 1가지이다. (참)
ㄴ. 네온(X)에는 홀전자가 존재하지 않는다. (거짓)
ㄷ. 원자가 전자 수는 인(P) 5개 < 황(S) 6개이다. (거짓)
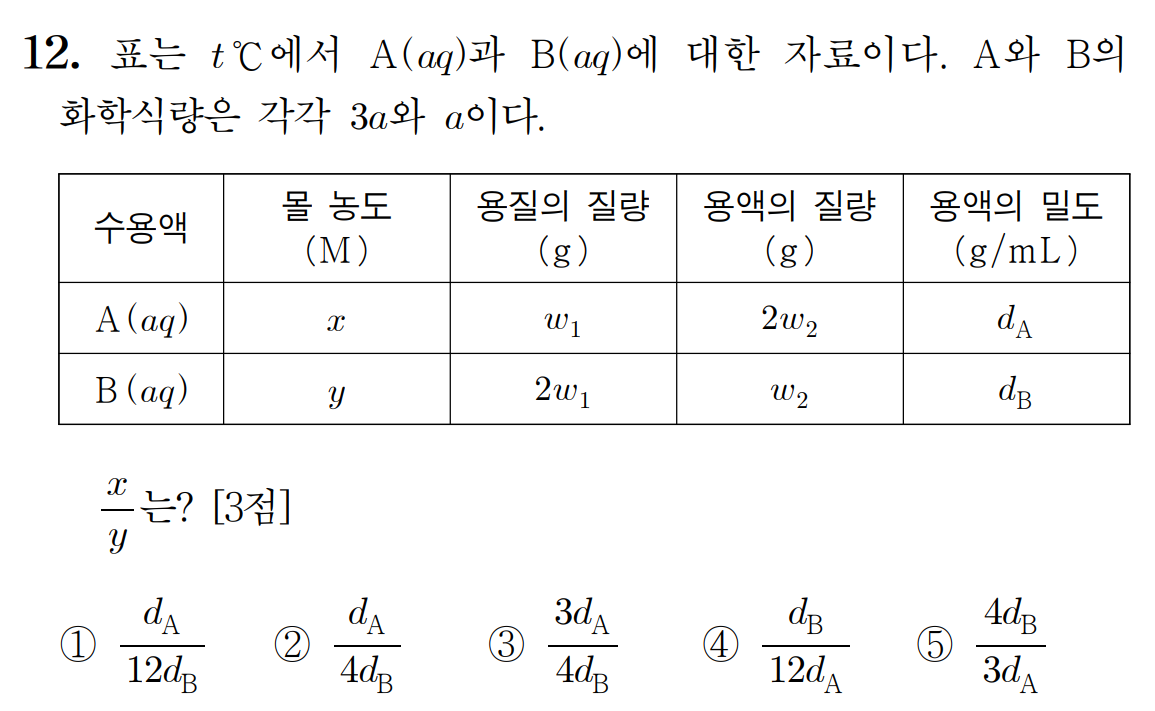
[12번 답] ① dA / 12dB
[풀이]
문제에서 묻고 있는 것은 용액 A와 B의 몰농도 비이다. 몰농도는 용질의 몰수에 비례하고, 용액의 부피에 반비례 한다. 용질의 몰수는 A = w1/3a , B = 2w1/a 이다. A 용액 내 용질 몰수가 1/3 일 때, B 용액 내 용질 몰수는 2 이다.
(용질 몰수, mol) x : y = (1/3) : 2 = 1 : 6 이다.
반면, 용액의 부피는 용액의 질량(g)을 용액의 밀도(g/mL)로 나누어 구할 수 있다. 따라서 A 용액의 부피가 2w2/dA 일 때, B 용액의 부피는 w2/dB 이다. 용액의 농도와 부피는 반비례하므로, 역수를 취하여 비교하면,
(부피 역수, 1/mL) x : y = dA/2 : dB 이다.
따라서 용질의 몰수와 용액 부피 역수 값을 곱해서 얻은 용액의 농도 x : y = dA/2 : 6dB 이며,
x / y = (1*0.5dA) / (6*dB) = dA / 12dB 이다.

[13번 답] ② ㄴ
[풀이]
유효핵전하는 같은 주기에서 원자번호가 커질수록 증가한다. 같은 주기에서 원자 번호가 1 증가하는 동안, 전자에 의한 가리움이 완전히 이를 상쇄해줄 수 없기 때문이다. 즉, 주어진 X, W, Y, Z 중에 원자 번호가 가장 큰 것은 Z이며, 원자 번호 순서는 다음과 같다.
X < Y < W < Z
원소 종류를 고려하지 않았을 때, 2주기 원소가 가질 수 있는 가장 큰 (n + l) 값은 3이며, 2p 오비탈에 해당한다. 바닥 상태의 전자 배치에서 갖는다고 했으므로, 3 개의 홀전자를 갖는 Z = 질소(N)임을 알 수 있다.
나머지 W, Y, X 는 질소보다 원자번호가 작은 원소들이다. W와 Y의 관계로부터 Y의 (ㄱ)은 2p가 아님을 알 수 있다. 만약, Y가 2p 오비탈에 2개의 전자가 들어있는 탄소라면, W를 정의할 수 없다. 따라서 W = 붕소(B), Y = 베릴륨(Be), X = 리튬(Li)이 되어야 한다.
X의 (ㄱ) = 2s , Y의 (ㄱ) = 2s , W의 (ㄱ) = 2p , Z의 (ㄱ) = 2p
ㄱ. Y는 베릴륨(Be)이다. (거짓)
ㄴ. 같은 주기 원자 반지름은 원자 번호가 커질수록 작아진다. 따라서 리튬(X) > 질소(Z) 이다. (참)
ㄷ. 같은 주기 내에서 전기 음성도는 주기율표의 오른쪽으로 갈수록 증가하며, 베릴륨(Y) < 탄소(W) 이다. (거짓)

[14번 답] ② 3/4
[풀이]
산화-환원 반응식 완성 과정에서 고려해야할 중요한 두 가지는, 반응 전후 관여한 전자수(산화수 변화)와 반응 전후 전하 균형이다. 이 두 가지를 신경쓰면, 미정계수법을 사용하지 않고도 손쉽게 반응식의 계수를 결정할 수 있다.
산화종 = M3+ → M4+ , 반응 전후 산화수 변화 = +4 - (+3) = +1
환원종 = Cl7+ → Cl- , 반응 전후 산화수 변화 = -1 - (+7) = -8
산화종과 환원종의 산화수 변화의 절대값(관여한 전자수)은 같아야 하기 때문에, 산화종의 계수에 8배를 해주어 두 화학종의 균형을 맞춰줄 수 있다.
a = e = 8 , b = d = 1
8M3+ + ClO4- + c H2O → Cl- + 8MO2+ + f H+
이후, 산소의 개수를 바탕으로 계수를 완성(i)시키거나, 반응 전후 전하 균형을 통해 계수를 완성(ii)시킬 수 있다.
i) 반응전 산소의 개수 = 4 + c 이며, 반응 후 산소의 개수는 8개 이므로, c = 4, f = 8
ii) 반응전 전하의 총합 = +24 -1 = +23이며, 반응 후 전하의 총합은 -1 +16 + f 이므로, f = 8 , c = 4
따라서 완성한 화학 반응식은 다음과 같으며,
8M3+ + ClO4- + 4H2O → Cl- + 8MO2+ + 8H+
문제에서 질문한 (d+f)/(a+c) = 3/4임을 알 수 이다.
(d+f) / (a+c) = (1+8) / (8+4) = 9/12 = 3/4

[17번 답] ③ ㄱ, ㄷ
[풀이]
(가)의 OH- 농도가 (나)에 비해 100배 진하다.
따라서 (가)와 (나)의 pOH 차이는 2이며, (가)의 pOH가 x일 때, (나)의 pOH는 x + 2 이다. 반대로 (가)의 pH가 y일 때, (나)의 pH는 y -2 이다.
y : y -2 = 7 : 3 이므로,7(y-2) = 3y 이고,
4y = 14 이므로, y = 3.5 이며,
(가)의 pH = 3.5, (나)의 pH = 1.5 이다.
ㄱ. (가)의 pH는 3.5이며, 액성은 산성이다. (참)
ㄴ. (나)의 pOH는 14 - 1.5 이며, 12.5 이다. (거짓)
ㄷ. (가) 용액의 pH는 3.5이며, H3O+ 농도는 10(-3.5) M 이다. 용액의 부피가 1 L라 할 때, H3O+ 몰수는 10-3.5 mol 이다. 반면, (나) 용액의 pOH는 12.5이며, OH- 농도는 10(-12.5) M 이다.
(나) 용액의 부피가 (가)의 100배이므로, 100 L라 하면, 용액 내 OH- 몰수는 10(-12.5) M * 100 L = 10(-10.5) mol 이다. 따라서 (가)의 H3O+ 몰수 / (나)의 OH- 몰수 = 10(-3.5) / 10(-10.5) = 107 이다. (참)
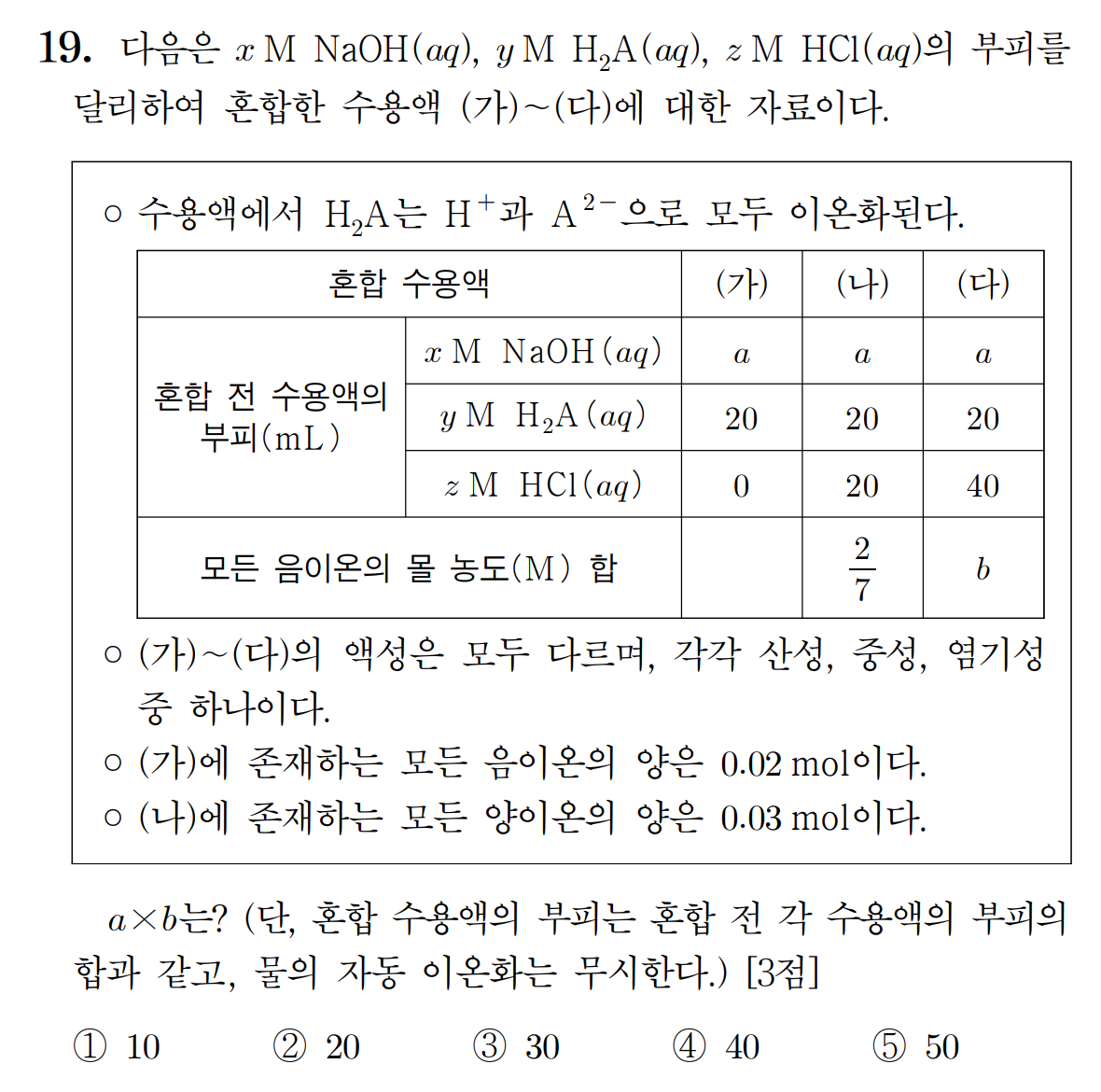
[19번 답] ① 10
[풀이]
(가) ~ (다) 혼합 용액의 액성이 모두 다르다는 조건을 주었기 때문에 비교적 접근하기 수월하다.
일정량의 염기에 (가) → (나) → (다)로 갈수록 산 수용액이 첨가되는 형태이므로, (가) = 염기성, (나) = 중성, (다) = 산성임을 알 수 있다. 완전히 중화가 일어난 (나) 용액을 통해 초기 OH-의 몰수는 ax [mmol] 이며, 첨가한 H+의 몰수인 40y + 20z [mmol]과 같다. (구경꾼 이온의 전하 균형으로 맞춰나가도 동일하다.)
ax = 40y + 20z [mmol]
(나) 용액은 완전히 중화가 일어났기에, 용액 내 존재하는 양이온은 Na+ 뿐이며, 해당 양이 30 [mmol] 임을 알 수 있다. 30 [mmol]은 초기 OH-의 몰수와 같다.
Na+ = OH- = ax = 40y + 20z = 30 [mmol]
(가)에 존재하는 음이온의 양이 20 [mmol]이라고 주어졌으며, 이는 초기 음이온 30 [mmol]에 비해 10 [mmol]이 감소했다. 이는 기존의 OH- 이온이 첨가된 A2-에 의해 대체되었음을 뜻하며, 2가 산 H2A가 10 [mmol]만큼 첨가되었음을 말한다. (2가 산이 첨가된만큼, 초기 이온 수에 비해 감소한다.)
40y = 20 mmol , y = 0.5 M
20z = 10 mmol , z = 0.5 M
(나) 용액의 부피는 a + 40 mL 이며, 용액 내 존재하는 음이온은 20y = 10 [mmol]의 A2- 과 20z = 10 [mmol]의 Cl- 가 전부이므로, 음이온 농도는 다음과 같으므로, 초기 NaOH의 부피를 구할 수 있다.
20 [mmol] / (a + 40) [mL] = 2/7 , a = 30 mL
(다) 용액의 부피는 a + 60 = 90 mL 이고, 산성 용액으로 모든 용액 내 존재하는 음이온은 20y = 10 [mmol]의 A2- 과 40z = 20 [mmol]의 Cl-가 전부이므로, 음이온 농도 b는 다음과 같이 표현할 수 있다.
b = 30/90 = 1/3 M
따라서 문제에서 요구하는 a * b = 30 * (1/3) = 10 이다.
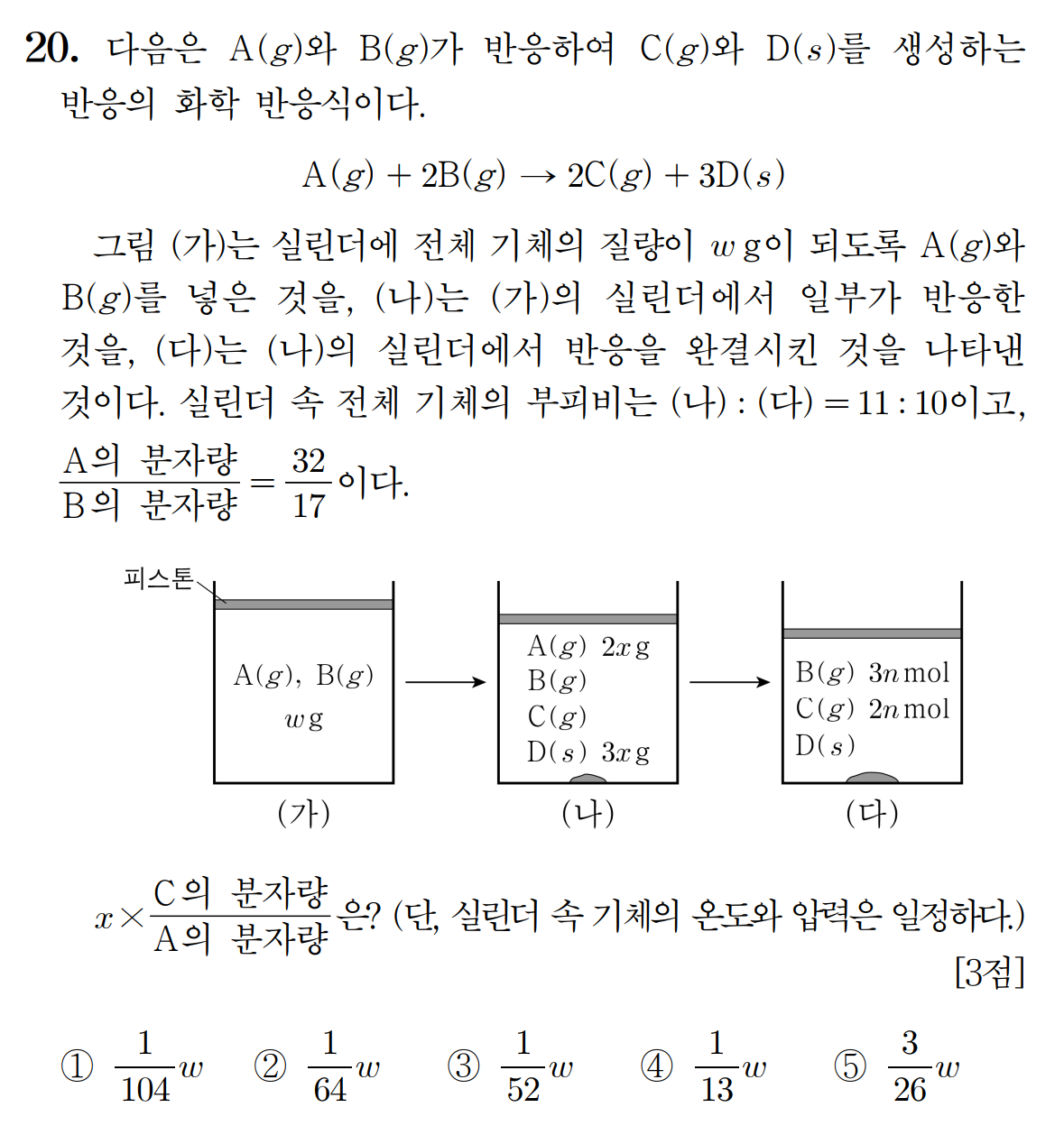
[20번 답] ③ w/52
[풀이]
(가)에서 시작한 반응이 (다)에서 완결되었다.
최종적으로 생성된 기체 C는 2n [mol]이며, 반응식의 계수 비에 따라 기체 A는 n [mol] , 기체 B는 2n [mol]이 반응했다. 따라서, 궁금하진 않지만 생성된 고체 D는 3n [mol]일 것이다.
과정 (다) : n 몰의 A가 완전히 반응하여 2n 몰의 C를 생성하고, B 3n 몰이 남아있는 상태 , 기체 몰수 = 5n [mol]
남아있는 B와 반응한 B의 몰수를 통해 초기 (가)에서 기체 B가 2n + 3n = 5n [mol] 있었음을 추측할 수 있으며, 전체 기체의 몰수 A + B = 6n [mol] 이다. 초기 질량 w [g]의 총 입자수는 6n [mol]이다.
과정 (가) : n 몰의 A와 5n 몰의 B가 있는 상태, 초기 반응물의 전체 질량 = w [g] = 6n [mol]
일정 온도, 압력 조건에서 실린더 부피는 내부 기체 몰수에 비례한다. 과정 (다) 부피가 10 일 때, 과정 (나) 부피가 11이므로, 과정 (나)의 남아있는 기체 입자수가 A + B + C = 5.5n [mol]임을 알 수 있다.
과정 (나) : 실린더 내 기체 A, B, C의 몰수 합 = 5.5n [mol]
화학 반응의 양적 관계를 살펴보았을 때,
1 mol 기체 A가 2 mol 기체 B와 완전히 반응하면, 2 mol 기체 C가 생성된다. 반응 전후 기체 몰수는 1 mol 감소한다. 2 mol의 기체 A가 4 mol의 기체 B와 완전히 반응하면, 4 mol의 기체 C가 생성된다. 반응 전후 기체 몰수는 2 mol이 감소한다.
과정 (나) → (다)에서 기체 몰수가 0.5n [mol] 감소했다는 것은 기체 A 0.5n [mol]이 반응했음을 뜻한다. A 기체 2x [g]은 0.5n [mol]에 해당한다. 기체 A의 분자량은 2x/(0.5n) = 4x/n [g/mol] 이다.
기체 A와 B 분자량은 32 : 17 비를 가지므로, 기체 B의 분자량은 17x/8n [g/mol] 이다. 초기 기체 A는 n [mol], 기체 B는 5n [mol]이 있었으므로, A 기체 n [mol] = 4x [g] , B 기체 5n [mol] = 85x/8 [g] 이 있었다.
(초기 질량) w [g] = ( 32x + 85x ) / 8 = 117x / 8 [g]
x = 8w / 117
과정 (나)는 A가 0.5n [mol] 반응한 이후 상태를 나타낸다. 따라서 현 시점에서 생성된 고체 D는 1.5n [mol]이다. 고체 D 1.5n [mol]의 질량이 3x [g]이므로, D의 화학식량은 3x/(1.5n) = 2x/n [g/mol] 이다. A, B, D의 화학식량을 알게 되었으므로, C의 분자량을 구할 수 있다.
A 분자량 = 4x/n , B 분자량 = 17x/8n , D 화학식량 = 2x/n
A + 2B = 2C + 3D 이며, 반응 전후 질량은 보존되므로, C의 분자량은 다음과 같다.
4x/n + (2*17x/8n) = 2*C + (3*2x/n)
2*C = (66x)/8n - [ (48x)/8n ]
2C = 18x/8n , C = 9x/8n [g/mol]
문제에서 요구하는 x * (C / A) 를 구해보면,
(8w /117) * [ (9x /8n) / (4x /n) ] = (8w /117) * (9/32) = w / 52
2024학년도 수능 6월 모의평가 화학1 3점 문항 풀이
- 끝 -
* 문제의 출처는 한국교육과정평가원입니다. 본문 설명 중 잘못된 부분에 대해 지적해주시면, 참고하여 수정 업데이트하도록 하겠습니다. 감사합니다.
'화학 > 기출풀이' 카테고리의 다른 글
| 2023학년도 대학수학능력시험(2022.11.17.) 화학2 풀이 [13번 ~ 20번] (0) | 2023.08.21 |
|---|---|
| 2023학년도 대학수학능력시험(2022.11.17.) 화학2 풀이 [1번 ~ 12번] (0) | 2023.07.15 |
| 2024학년도 수능 6월 모의평가(2023.6.1.) 국어 지문 [8~11번] (0) | 2023.06.01 |
| 2023학년도 3월(3.23.) 고3 전국연합학력평가 국어 [14~17번 지문] (0) | 2023.03.30 |
| 2022학년도 10월(10.12.) 고3 전국연합학력평가 화학1 3점 문항 풀이 (0) | 2022.12.15 |



