2025학년도 대학수학능력시험(2024.11.14.) 화학2 3점 문항 풀이
2025학년도 대학수학능력시험(2024.11.14.) 화학2 3점 문항 풀이
전반적으로 1, 2면은 휙휙 넘길 수 있지만, 살짝 머뭇거리게 만드는 요소가 살짝살짝 섞여 있어서 중위권 학생들의 실수 또는 어려움을 유발할 수 있었고, 3-4면은 생각해 볼 만한 문제들이 여럿 섞여 있었다. 매년 평가원에서 섭외한 출제위원들이 똑같지는 않기 때문에 문제 스타일이 달라지는 것이 어찌 보면 당연할 수도 있는데, 킬러문항 배제를 선언한 이후로 특히나, 문항이 유형화되고 고착화되는 것을 경계하고 있음이 느껴진다. 개념을 쌓는 단계를 가볍게 여기고, 기출 풀이와 유형 반복만으로 일정 등급 이상을 받는 것을 막겠다는 의지가 느껴진다. 개인적으로는 바람직한 방향이라고 생각한다. 최상위권은 어쨌든 할만했고, 중상위권에게는 다소 어렵다는 느낌을 주면서, 중하위권에게는 생소함을 안겨줄 수 있는, 나름 괜찮은 문제들이 포함된 시험이었다고 생각한다.
이번 2025 화학2의 3점 문항은 2번, 5번, 6번, 10번, 11번, 13번, 14번, 17번, 19번, 20번이다.

2번 답: ④ (ㄱ) 체심, (ㄴ) 공유
5번 풀이:
철은 체심입방구조의 금속결정, 다이아몬드는 공유결정, 드라이아이스는 면심입방구조의 분자결정이다.

5번 답: ③ (ㄱ) 증가, (ㄴ) B > C
5번 풀이:
(가)의 전자 이동 방향을 통해 금속의 이온화 경향성은 B > A 이다. (나)에서 A 전극의 질량이 감소(산화)하므로, 금속의 이온화 경향성은 A > C 이다. 이를 종합했을 때, 금속의 이온화 경향성은 B > A > C 이다.
(나)에서 A는 산화하여 A2+ 이온을 생성하므로, A2+ 농도는 증가한다.

6번 답: ① (ㄱ) 100, (ㄴ) 260
6번 풀이:
X의 증기압은 대기압보다 660 mmHg 작다. PX = 760 - 660 = 100 mmHg이다. Y의 증기압은 대기압보다 400 mmHg 작다. PY = 760 - 400 = 360 mmHg이다. 그리고, PY = PX 보다 h mmHg 만큼 증기압이 크다. 따라서 h = 360 - 100 = 260 mmHg

10번 답: ② a + 530
10번 풀이:
x는 F2의 결합 에너지이다. 그런데 중요한 것은 문제에서 별다르게 F2에 관한 반응식을 끌어낼 수 있는 요소를 제시하지 않았다. 이것을 빠르게 찾아낼 수 있는가에 달려있는 문제다.
2HOF → 2HF + O2 반응의 ΔH = a = (HF의 생성엔탈피*2) + (O2 생성엔탈피) - (HOF의 생성엔탈피*2) 이다. O2와 HOF의 생성엔탈피가 각각 0 kJ과 - 87 kJ이므로, a = 2HF + 0 - (-87*2) 이며, (HF의 생성 엔탈피*2) = a - 174 kJ 이다.
2몰의 HF가 생성되는 반응식을 나타내면, H2 + F2 → 2HF 이며, 이는 1개의 H-H 결합을 끊고(+ 436 kJ), 1개의 F-F 결합을 끊고(+ x), 2개의 H-F 결합을 생성하는(- 570*2) 과정이다. 식으로 나타내면 다음과 같다.
a - 174 = 436 + x - (570*2)
x = a +1140 + 174 - 436 = a + 530 이다.

11번 답: ① (ㄱ) t > -56.6, (ㄴ) P1 = P2
11번 풀이:
* 별도 글(335)을 참고해 주기 바랍니다. https://stachemi.tistory.com/335
2025학년도 대학수학능력시험(2024.11.14.) 화학2 풀이 [11번]
2025학년도 대학수학능력시험(2024.11.14.) 화학2 풀이 [11번] 11번 답: ①11번 풀이: 11번은 상평형 문제인데 개인적으로는 괜찮은 것 같다. 다수 학생들이 단순히 온도가 일정하니까 단연히 증기
stachemi.tistory.com
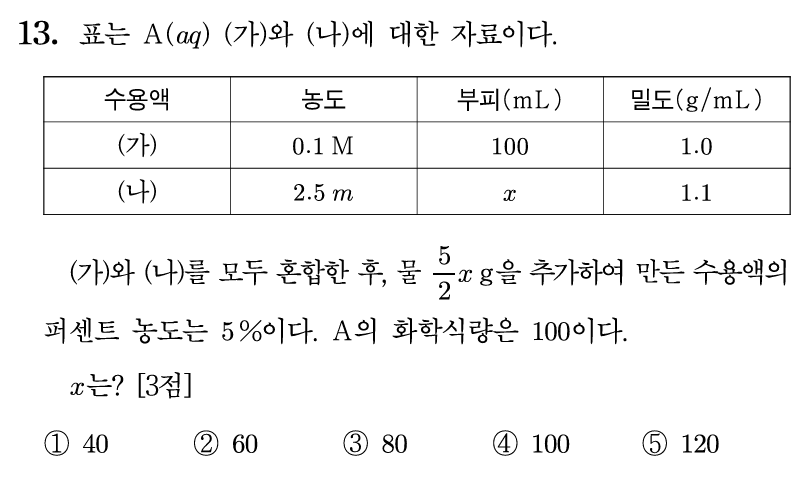
13번 답: ④ 100
13번 풀이:
더 간단한 풀이 방법을 고민하지는 않았다. 처음 시도했던 방법을 남긴다. 마지막에 물 2.5x [g]을 추가하고, 용액의 농도가 5%라고 했으므로, 그냥 퍼센트 농도의 혼합이 가장 빠르지 않을까 해서 단순 퍼센트 농도 합산으로 접근했다.
(가) 수용액은 농도 = 0.1 M, 용액 = 100 mL 이므로, 용질은 10 mmol = 1 g에 해당한다. 밀도가 1 [g/mL]이므로, 용액 질량은 100 [g]이고, % 농도는 1%이다.
(나) 수용액은 농도가 2.5 m이다. 용매 1 kg에 2.5 mol이 녹아 있는 상태다. 용질 2.5 mol은 250 [g]에 해당하고, 용액 전체가 1250 [g]이라면, 용질이 250 [g] 존재하는 것이니 % 농도로는 250/1250 분율의 20% 수용액이다. 다만 전체 부피가 x mL 이므로, 전체 용액 질량은 1.1x [g]이고, 실제 용질은 1.1x/5 [g] 이다.
(가)와 (나) 그리고 물 2.5x [g]을 추가 혼합하여 전체 퍼센트 농도가 5%가 되었다.
용질 전체 양 = 1 + (1.1x/5) [g]
용액 전체 양 = 100 + (1.1x) + 2.5x = 100 + 3.6x [g]
5% 농도 분율은 5/100 이므로, 5(100 + 3.6x) = 100(1+(1.1x/5)) 이다. 풀어 정리하면, 500+18x = 100 + 22x 이고, x = 100이 된다.
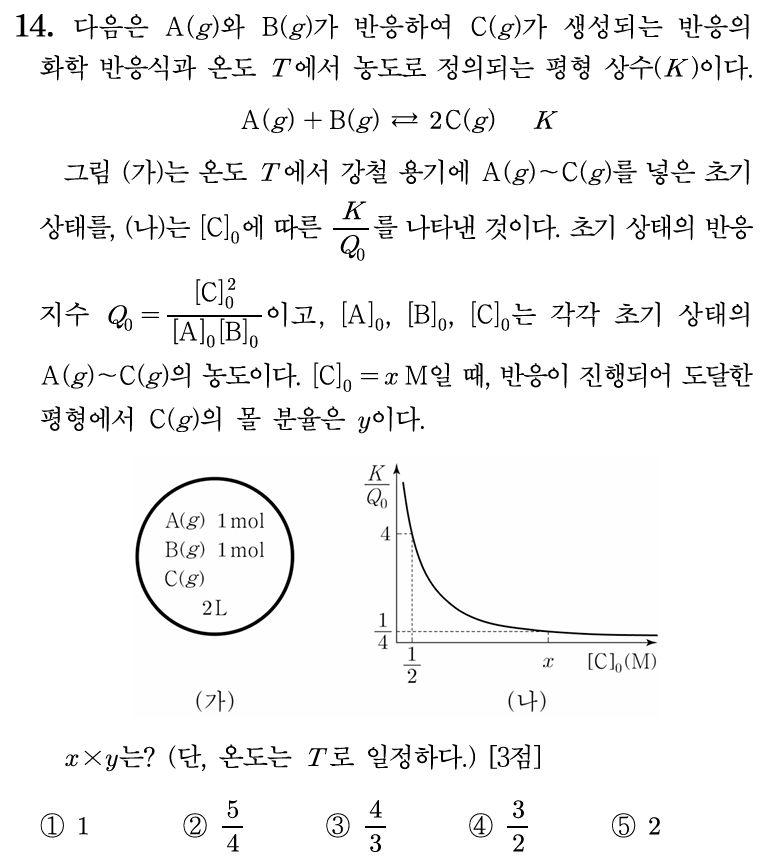
14번 정답: ① 1
14번 풀이:
K /Q 비율을 그래프로 제시했다. K /Q 가 1보다 크다는 것은 정반응 우세, K /Q 가 1보다 작다는 것은 역반응 우세인데, 이 문제에서는 적극적으로 활용되는 정보는 아니다. 오히려, 초기 A와 B의 몰수가 모두 1 mol로 주어졌는데, 전체 부피는 2 L이므로, 평형상수 계산 과정에서 초기 A, B의 몰농도가 0.5 M씩임을 주의해야 한다.
활용할 수 있는 지점이 [C]0 = 0.5 M, K /Q = 4 인 지점이므로, 초기 농도 [A]0 = 0.5 M, [B]0 = 0.5 M 를 이용해서 Q 를 계산해 보면, Q = 1 이다. K /Q = 4 이므로, 해당 온도에서의 K = 4이다.
일정 온도 조건에서 K 는 변함없으므로, K /Q = 1/4 지점에서의 Q = 16이다. Q = x2/(0.5)2이므로, [C]0의 초기 농도 x = 2이며, C의 초기 몰수는 2x = 4 mol 이다.
이제 평형에서의 농도를 구하면,
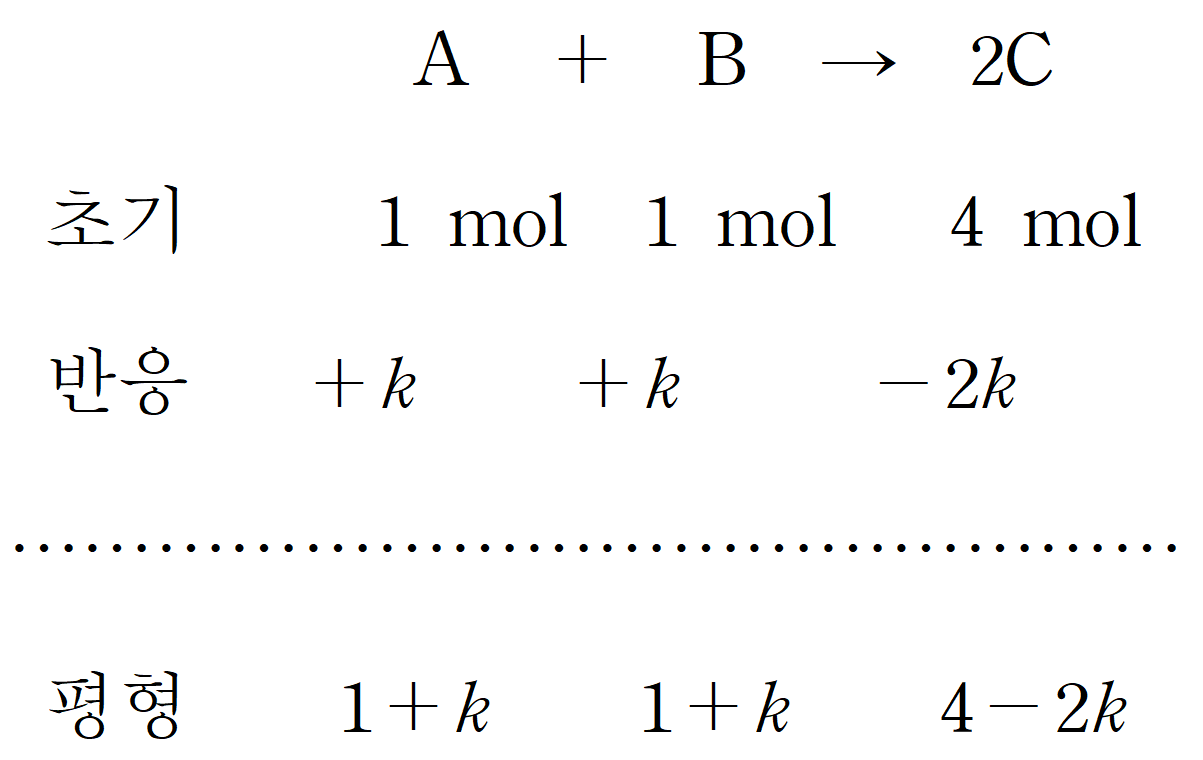
평형 상수 K = 4 이므로, [ (2-k) / 0.5(1+k) ]2 이고, (4-2k)/(1+k) = 2 이다. k = 1/2 이다.
따라서 평형에서의 전체 몰수는 1+1+4 = 6 mol 이며, C의 몰수는 4 - 1 = 3 mol 이므로, C의 몰분율은 1/2 이다.
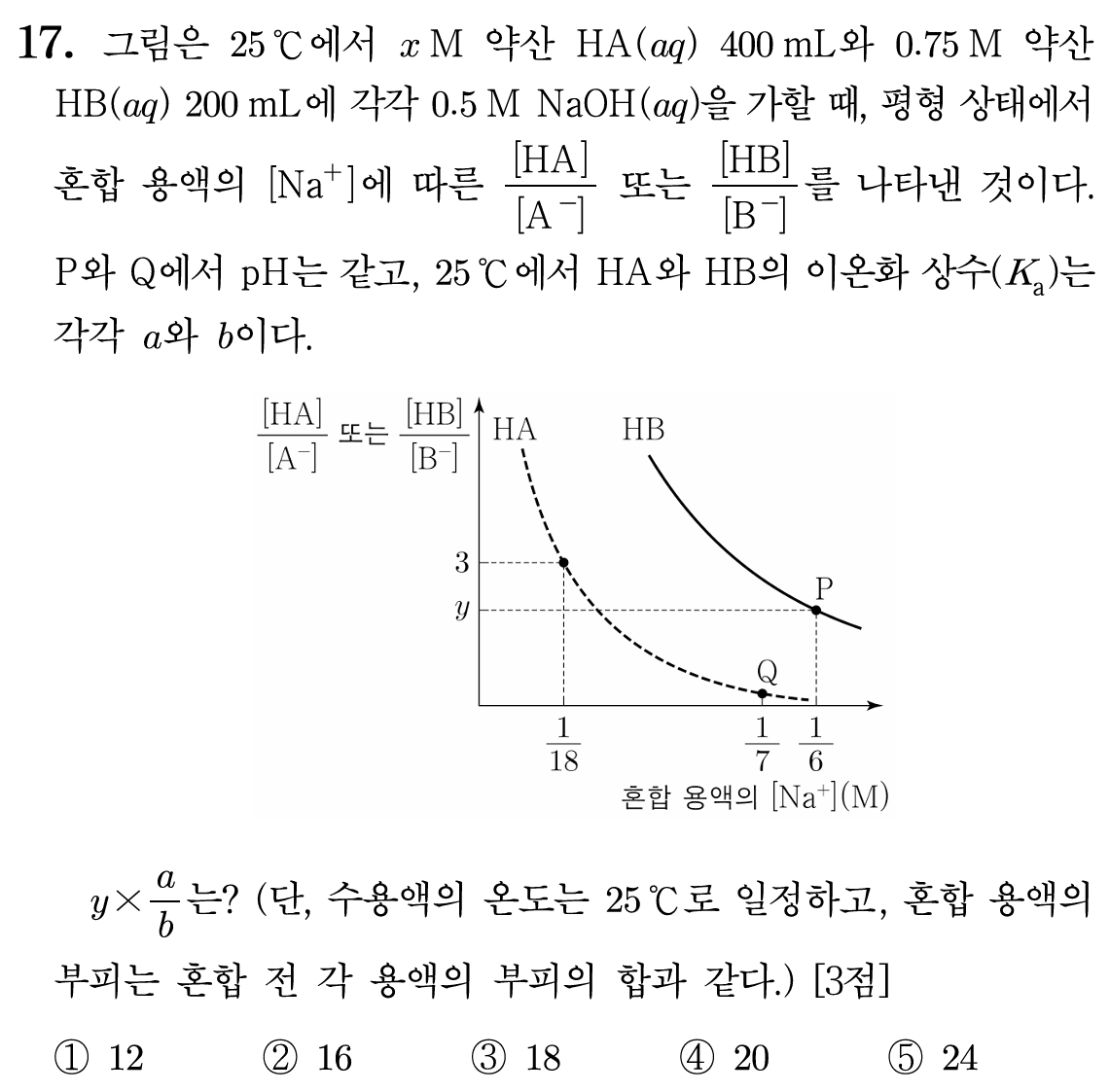
17번 정답: ② 16
17번 풀이:
그래프의 x축은 첨가한 염기의 몰수와 전체 부피, y축은 약산의 분율항이다. y = 3인 지점은 HA : A-의 비율이 3 : 1인 지점으로 당량점의 1/4 지점임을 알 수 있다. 그런데, Na+의 농도가 1/18이므로, 첨가한 NaOH의 부피가 k mL라고 하면,
Na+의 몰수 = 0.5k mmol , 전체 용액 부피 = 400+p 이며, 0.5k / (400+k) = 1/18 이고, k = 50 이다. 즉, 첨가한 NaOH의 몰수는 0.5 M * 50 mL = 25 mmol 이다. 이 지점은 1/4 당량점이며, 완전히 중화되기 필요한 몰수는 100 mmol이며, 필요한 NaOH의 부피는 200 mL라는 뜻이다. 따라서 초기 HA의 몰농도 x = 2.5 M 이다.
HA의 Na+의 몰농도가 1/7인 Q 지점도 같은 방식으로 해결하면, 첨가한 Na+의 몰수 = 0.5q mmol, 전체 용액 부피 = 400+q mL 이므로, 0.5q / (400+q) = 1/7 이고, 3.5q = 400+q , 2.5q = 400 , q = 160 mL 이다. NaOH가 160 mL 첨가되었다.
NaOH 160 mL 첨가된 지점은 중화점의 8/10 지점으로 Q지점에서의 HA의 Ka = a = [H+]*(8/2) 이다.
HB는 몰농도와 부피가 모두 주어졌으므로, 초기 산의 몰수는 0.75 M * 200 mL = 150 mmol이다. 혼합 용액에서의 Na+ 농도를 이용해 정리해보면,
Na+ 몰수 = 0.5p mmol , 전체 용액 부피 = 200+p 이며, 0.5p / (200+p) = 1/6 이고, p =100 이다. NaOH 100 mL 첨가되었을 때는 전체 당량점의 2/3 지점이며, B- : HB = 1 : 2 인 지점이 된다. 따라서 y = 2 이다.
P지점에서의 HB의 Kb = b = [H+]*(1/2) 이 된다.
P지점과 Q지점의 [H+]가 같으므로, 2b = a/4 이고, a = 8b 이다.
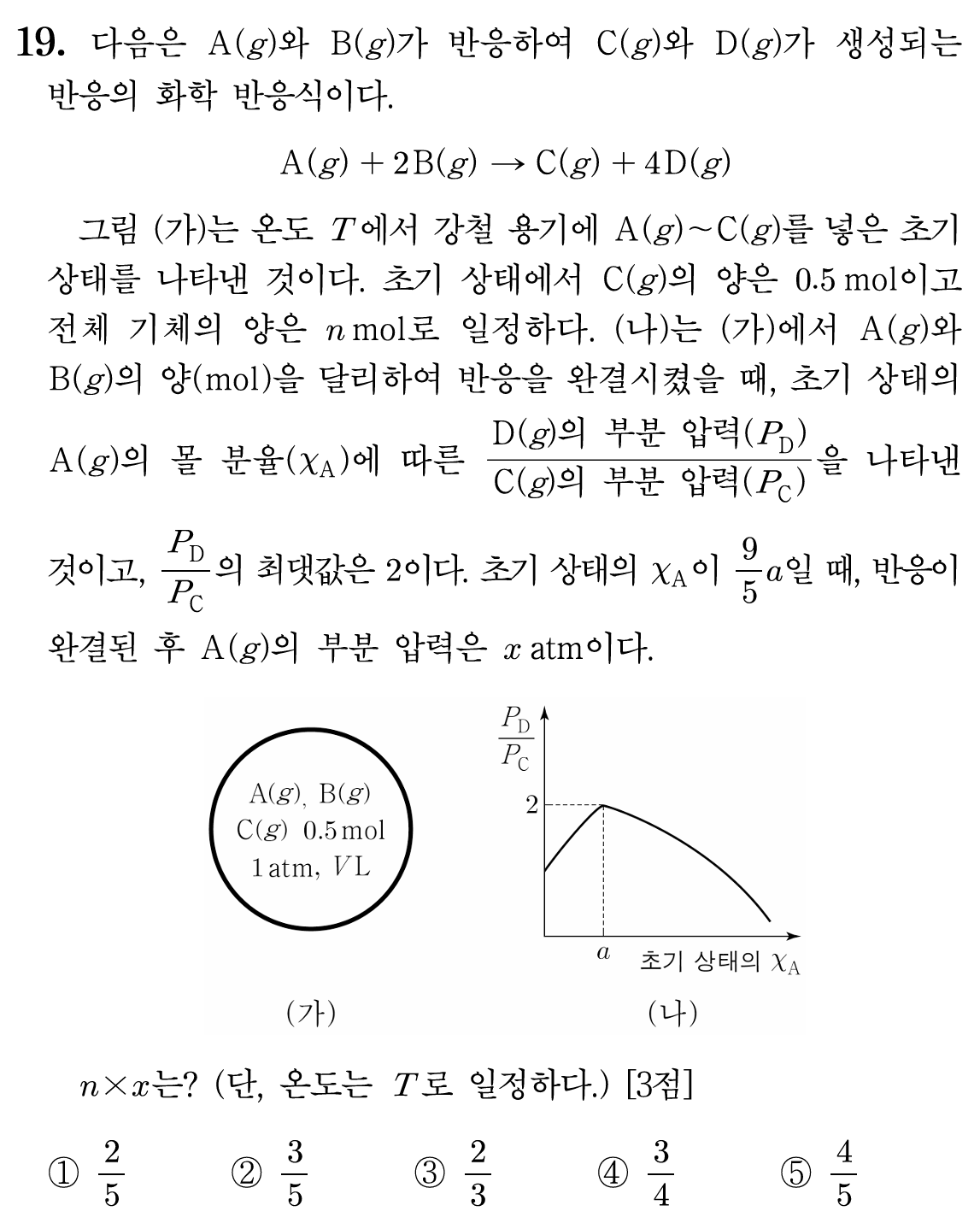
19번 정답: ② 3/5
19번 풀이:
온도가 T로 일정하고, 부피가 V로 일정하다. 기체의 압력은 오직 몰수에만 의존한다.
그림 (가)에서 초기의 A, B, C의 몰수의 합은 n mol로 일정하다. 초기 C의 몰수가 0.5 mol이고, (나) 그래프에서 최대로 가질 수 있는 nD : nC가 2 : 1 이므로, 반응이 완결된 이후 C = 1 mol, D = 2 mol이 된다.
반응한 C의 몰수를 y라 했을 때, C = 0.5 + y , D = 0 + 4y 이며, D = 2C 이므로, y = 0.5
C가 0.5 mol 생성(y)되었다는 뜻은 계수비에 따라 반응한 A가 0.5 mol, B가 1 mol이며, (나)의 그래프는 A, B의 비율이 다를 뿐, 모두 일정 몰수의 반응물에 의한 결과이므로, D와 C의 비율이 최대인 지점(2)이 두 반응물 A, B가 남지 않고 완전히 모두 반응한 지점임을 알 수 있다.
즉, 초기 A = 0.5 mol, B = 1 mol이었으며, 전체 몰수는 C를 포함하여 n = 2 mol 이다. 이때, 초기 A 몰분율은 a = 0.5/2 = 1/4이다. 초기 압력이 1 atm 이었으므로, 전체 몰수(2 mol)의 절반에 해당하는 압력 값(1 atm)을 가짐을 알 수 있다.
a = 1/4 이므로, 초기 상태의 A 몰분율이 9a/5 = 9/20이며, 전체 몰수는 2 mol로 일정하므로 A는 0.9 mol이다. B는 자연스레 0.6 mol이 된다. 이 경우 반응을 진행하면, B 0.6 mol이 완전히 소진되며, A는 0.3 mol만 반응하여 0.9 - 0.3 = 0.6 mol이 남는다. C는 0.3 mol이 생성되어 총 0.5 + 0.3 = 0.8 mol이 되며, D는 1.2 mol이 생성된다. 정리하면,
A = 0.6 mol, C = 0.8 mol, D = 1.2 mol 이며, XA = 6/26
문제에서 요구하는 것은 A의 부분압력은 PA = 전체 압력 * XA이다. 전체 몰수가 2.6 mol 이므로, 전체 압력은 1.3 atm이고, PA = 1.3*6/26 = 3/10 이다.
따라서 n * x = 2 * 3/10 = 3/5 이다.

20번 정답: ① 6/5
20번 풀이:
사실, 화학2에서의 화학반응속도론은 기승전 '반감기'이다. 1차 반응으로 제한된 이상 반감기를 활용한 문제를 벗어날 수가 없다. 개인적으로 수능에서 화학반응속도론은 이제 수명을 다했다고 본다. 오히려 3면의 12번 문제가 더 깔끔했다.
실험 (가)와 (나)에서 반응물과 생성물의 몰비가 7배 차이나는 지점을 통해 반감기를 찾아야 한다. 나는 문제를 통찰하는 직관이 없으니 하나씩 해봐야 했다. A의 초기 몰수는 넉넉하게 64로 가정했다.(엄밀하게는 64k가 맞겠지만...) 지면이 넓었어도, 시간이 충분하게 남았어도 침착하게 비례 관계에서 실수하지 않고, 차분하게 풀어냈을 자신은 없다.
[1] 실험 (가)와 (나)의 반감기 찾기
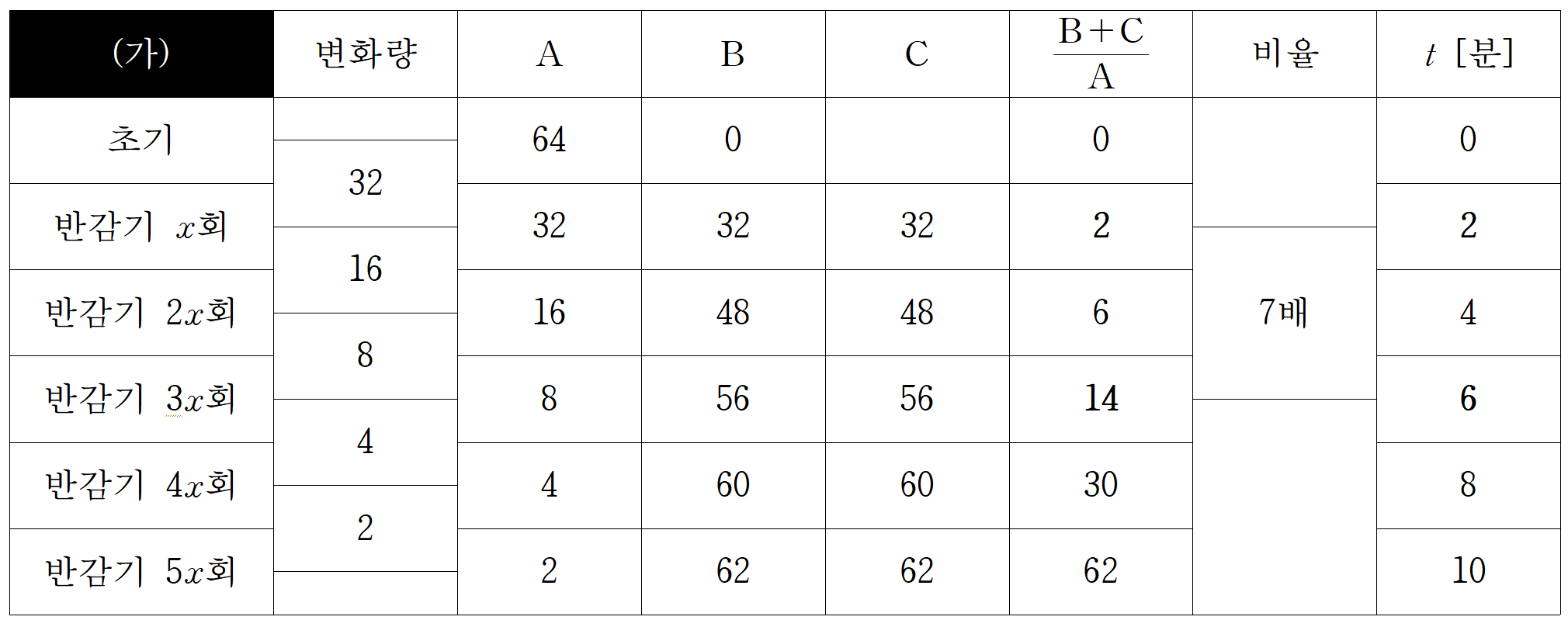
실험 (가)의 반감기는 2분(x=2)이다. 반감기 x회 거쳤을 때, 생성물/반응물 비가 2a, 3x회 거쳤을 때, 14a로 7배 차이 난다.
같은 방법으로 (나)에 대해서도 하나씩 해보자. 다른 점은 초기 B가 존재한다는 것이며, 0분에서의 반응물 생성물 비가 b라는 조건을 바탕으로 B의 초기 몰수는 64b로 설정했다.
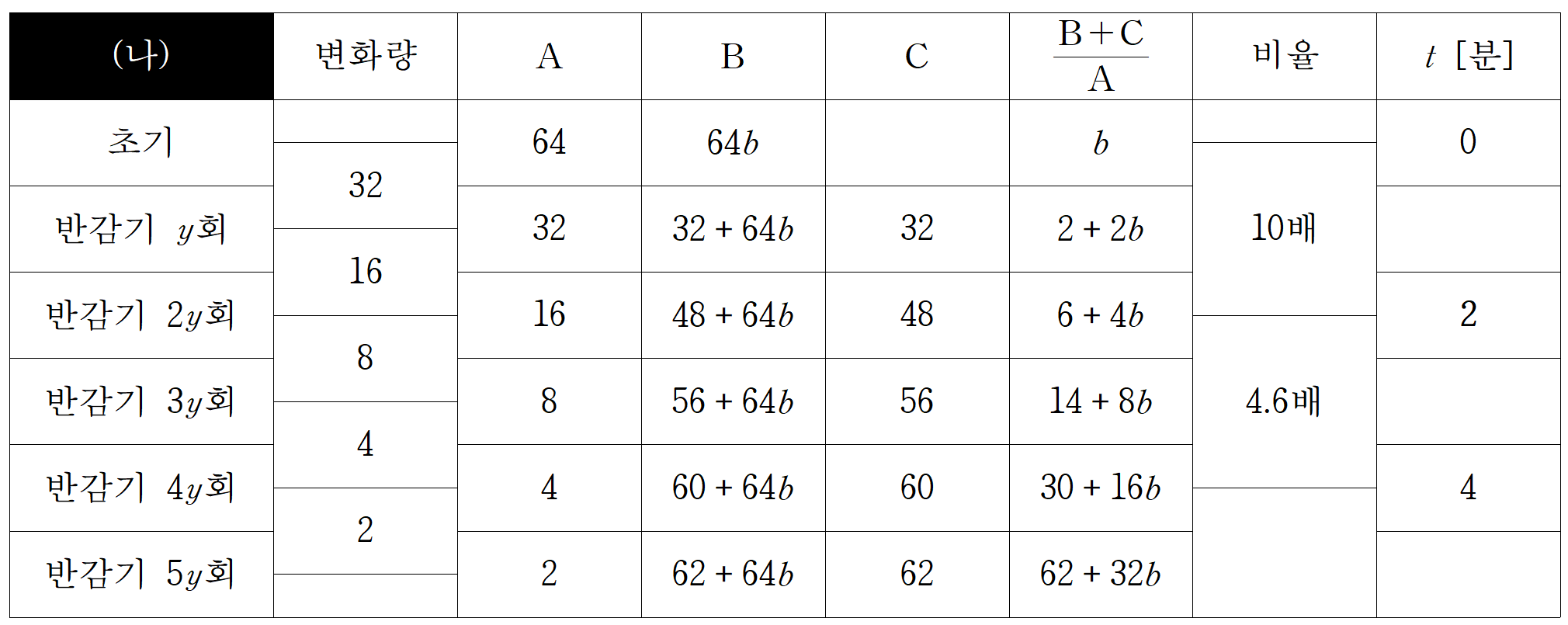
실험 (나)의 반감기는 1분(2y=2)이다. 비율 식이 복잡하기에 b값을 그대로 두고는 비례관계가 잘 보이지는 않는다. b에 1을 넣었을 때, 초기 생성물/반응물 비가 1, 2y회 거쳤을 때, 6+4=10으로 10배 차이 난다. b가 1이라는 뜻은 초기 A 64라면, B도 64로 같은 몰수만큼 들어있었다는 뜻이 된다. 초기 몰수가 6n이라 했으니 A와 B가 각각, 3n씩 들어있는 것과 같다.
[2] 실제 몰수로 변환해서 부분압력 관계 찾기
PV=nRT에서 강철 용기로 V가 일정하다. P = nT로 생각할 수 있다. (가)와 (나)의 몰수를 비교하기 위해서는 표에서 주어진 n을 사용해서 나타내야 한다.
(가)의 초기 몰수는 5n이다. 우리가 사용할 시간은 2분이다. (가)의 2분은 반감기를 한 번 거쳤을 때, 생성되는 B의 몰수이다. 2분에 남아있는 A = 32 이며, 생성된 B 역시 같은 32이다. (가)에서는 64 = 5n이므로, 5n/2에 해당한다. (가)의 2분에서의 B의 부분 압력은 온도 T1을 곱한 값이며, PB = (5n/2)*T1 이다.
(나)의 초기 몰수는 A = 3n, B = 3n 이다. 64을 3n이라 했으므로, 반감기를 2회 거친 이후 A는 3n/4이 남았다. 마찬가지로 (나)의 2분에서의 A의 부분 압력은 온도 T2을 곱한 값이며, PA(나) = (3n/4)*T2 이다.
PB / PA = 3 이라고 했으므로, T1 = 9, T2 = 10에 해당한다.
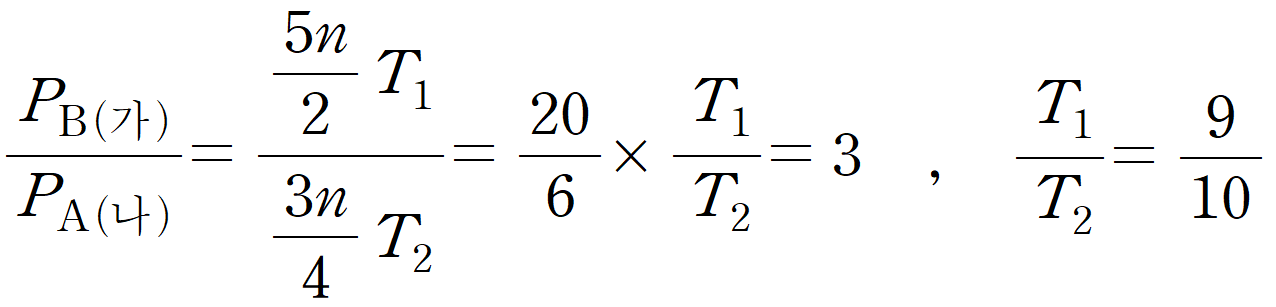
[3] 최종 질문 찾기
최종적으로 4분에서의 (가)와 (나)의 C에서의 부분 압력 비를 묻고 있으므로, 같은 방법으로 구해보면, (가)에서 생성된 C는 48이며, 64 = 5n 관계에 의해, 15n/4 이다. (가)의 온도 T1은 9이다. (나)의 4분에 생성된 C는 60이며, 64 = 3n의 관계에 의해 생성된 몰수는 45n/16 이다. (나)의 온도 T2는 10이다.
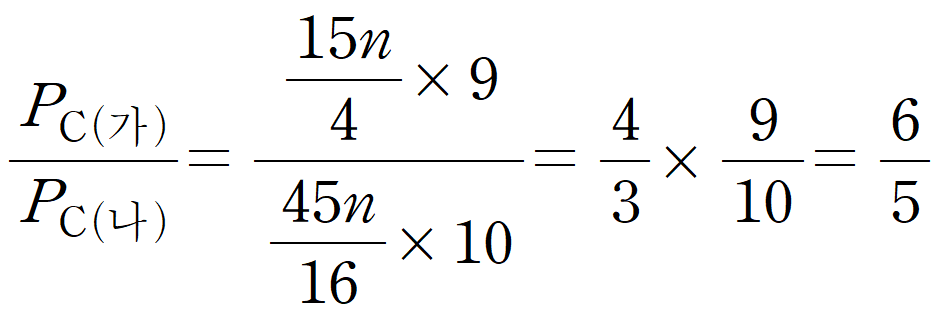
끝
* 위 문제의 출처는 한국교육과정평가원이며, 정답 및 해설 강의는 EBSi 사이트에서도 확인하실 수 있습니다.
