2023학년도 PEET 화학추론(일반화학) 기출문제 풀이 (21번~25번)

화학/기출풀이

2023학년도 PEET 화학추론(일반화학) 기출문제 풀이 (21번~25번)

stachemi 2024. 6. 15. 10:35

2023학년도 PEET 화학추론(일반화학) 기출문제 풀이 (21번~25번)

이전 문항 풀이는 아래 링크를 이용해주세요.

2023학년도 PEET [1번~10번] https://stachemi.tistory.com/310

2023학년도 PEET [11번~20번] https://stachemi.tistory.com/317

21번 답: ⑤ ㄱ, ㄷ

풀이:

압력 평형 상수가 주어지고, 마지막 보기에 압력 평형 상수를 구하라는 지문이 있어서 평범한 평형 문제인 줄 알았는데, 풀고 나니 기체 법칙 문제에 가까운 것 같다. 정석 적인 풀이가 이 방법이 맞는지는 잘 모르겠다. (뭔가 다른 풀이가 있을 듯 한 느낌이 크다...)

부피가 다른 여러 개의 강철 용기에서 일어난 평형 반응이라고 제시되어 있다. 그런데, 온도를 일정하게 유지한 채로 초기 부피 2 L였던 용기를 점차 3 L, 4 L로 늘려갔다고 생각해도 결과는 다르지 않을 것이다.

초기 넣어준 고체 AB₂의 양을 모르기 때문에, 그래프를 통해 확인할 수 있는 변화량으로 접근해보자.

2 L 용기에 0.2 mol 존재하던 AB₂ 고체가 3 L로 부피가 늘어나자 0.1 mol이 반응하여 0.1 mol만 남았다. 화학 반응식의 계수 비에 따라, 새로 생겨난 A₂ 몰수는 0.05 mol이고, B₂ 몰수는 0.1 mol이다. 부피 변화(ΔV )가 1 L 당에 전체 기체 몰수 변화(Δn)는 0.05 + 0.1 = 0.15 mol 이다.

PΔV = ΔnRT , P = 0.15*RT 이므로, 점 P에서의 압력 P 는 6 기압이다. 반응 후 생성된 A₂와 B₂의 몰비 언제나 1 : 2의 비를 만족해야 하므로, 점 P 점에서 A의 부분압 P_A = 2 기압, B의 부분압 P_B = 4 기압이다.

용기 부피가 2 L → 4 L가 되면 고체 AB₂ 0.2 mol을 모두 소진한다. 부피 변화 ΔV = 2 L, 몰수 변화 Δn = 0.1 + 0.2 = 0.3 mol 이므로, PΔV = ΔnRT , P = 0.3*RT / 2 = 6 기압이 된다. 온도 변화 없이 부피를 5 L로 변화시키면, 점 Q에 도달하는데, 더 이상의 반응은 진행되지 않고, 보일 법칙에 따라 압력만 감소한다.

P * V = P ' * V ' , 6 기압 * 4 L = P ' * 5 L , 점 Q에서의 전체 압력 P ' = 24/5 기압

ㄱ. 각 지점에서 기체 몰수(n)는 부분 압력(P )과 부피(V )를 통해 구할 수 있다. 점 P에서의 A₂ 기체 부분 압력 P_A = 6 기압*(1/3) = 2 기압이고, n ∝ 2 기압 * 3 L ∝ 6 mol 이다. 점 Q에서는 A₂ 기체 부분 압력 P_A' = 24/5 기압*(1/3) = 8/5 기압이고, n ∝ (8/5) 기압 * 5 L ∝ 8 mol 이다.

점 P의 n_A / 점 Q의 n_B = 6/8 = 3/4 (참)

ㄴ. 점 P에서의 기체 B₂의 부분 압력 P_B = 6 기압*(2/3) = 4 기압이고, 점 Q에서의 기체 B₂의 부분 압력은 24/5 기압 * (2/3) = 16/5 기압 이다.

점 P의 P_A / 점 Q의 P_B = 4 / (16/5) = 20/16 = 5/4 (거짓)

ㄷ. 온도는 T 로 일정하므로, K_p는 그래프의 아무 지점이나 선택해서 계산해도 무방하다. 점 P에서의 부분 압력을 이용하면, P_A = 2 기압, P_B = 4 기압이므로,

K_p = (P_A)(P_B)² = 2 * (4)² = 32 (참)

22번 답: ② ㄴ

풀이:

문제 구성에서 왜 굳이 고체 B가 포함되었는지 의문이다. 풀이를 작성하고 보니, 과정 중에 고체 B를 전혀 고려하지 않았다. 이하 작성된 풀이가 잘못되었거나, 미처 생각하지 못한 놓친 부분이 있을 수도 있겠다. 앞선 문제와 달리 고체의 부피를 무시한다는 단서 조항이 없어서 뭔가 찜찜하다.

한 분자의 기체 A가 두 분자의 C로 분해되는 반응이라 생각하면, 정반응은 입자수가 많아지는 반응이다. 그래프 x축은 외부압이며, 동시에 평형을 이루는 실린더 내부의 기체 전체 압력(P_tot)이기도 하다. 전체 압력이 2일 때, 어떤 기체의 부분 압력 P₁이 1이면, 나머지 기체의 부분 압력도 1이다.

ㄱ. 즉, 외부압이 2 기압일 때, 두 기체의 몰수는 서로 같다. 예를 들어 0.75 mol의 A 기체 중 0.25 mol이 분해되어 0.5 mol의 기체 C이 생성되고 A 기체 0.5 mol이 남아있는 상황과 같다. 온도 T₁에서의 압력 평형 상수는 일정하므로, 이 때의 부분 압력 값으로 K_p 값을 구하면, (P_C)²/(P_A) = 1이다. (거짓)

ㄴ. 위 반응은 ΔH > 0 인 반응으로, 흡열 반응이다. 외부 압력이 4 기압일 때, 기체 A, C의 부분압이 모두 2 기압일 때, 평형 상수 K_p 값을 구하면, (P_C)² / (P_A) = 4/2 = 2이다. 정반응이 흡열 반응인데, K_p 값이 증가했다는 것은 T₂의 온도가 T₁ 보다 높다는 뜻이다. (참)

ㄷ. 온도 T₁, 2기압 조건에서 기체 A와 C가 각각 1기압씩 부분 압력을 유지하고 있으며, 이 경우 몰 비는 1 : 1 이다. 그런데, 압력을 4 기압으로 올렸더니 P₁의 부분 압력이 2기압 보다 작아졌다. 몰비가 1보다 작아졌고, 그래프의 기울기가 1보다 작아졌다. 압력을 높이면(부피를 줄이면), 기체 입자수가 줄어드는 방향으로 평형은 이동하고, 역반응이 우세하게 진행된다. 생성물의 몰비는 1보다 작아지고, 반응물의 몰비는 1보다 커질 것이므로, P₁은 기체 C, 생성물의 부분 압력이다. (거짓)

23번 답: ⑦ ㄱ, ㄴ, ㄷ

풀이:

광학 이성질체(optical isomer)는 거울상 이성질체(enantiomer)로 불리기도 하며, 서로 포개지지 않는다. 입체 이성질체(stereo isomer)는 광학 이성질체와 부분 입체 이성질체(diastereomer), 기하 이성질체(geometric isomer) 등 공간 배열에 의한 구조의 차이를 갖는 이성질체 모두를 포함한다.

[M(NH₃)₃(H₂O)₃]²⁺는 간단하게 Ma₃b₃ 타입이라 볼 수 있으며, 입체 중심을 갖지 않는다. 그러나 연결 위치에 따라 faical과 meridional의 두 가지 기하 이성질체를 갖는다.

[MQ₃]^-는 M(AB)₃ 타입이다. 두 자리 리간드인 8-하이드록시퀴놀린(8-hydroxyquinoline) 음이온의 경우 금속과 직접 결합하는 원소가 질소(N)와 산소(O) 두 가지이다. 이에 결합 원소의 배치에 따라 facial과 Meridional의 두 가지 기하 이성질체를 갖고, 각각의 기하 이성질체는 회전 방향이 다른(선풍기 날개 형태) 광학 이성질체를 갖는다.

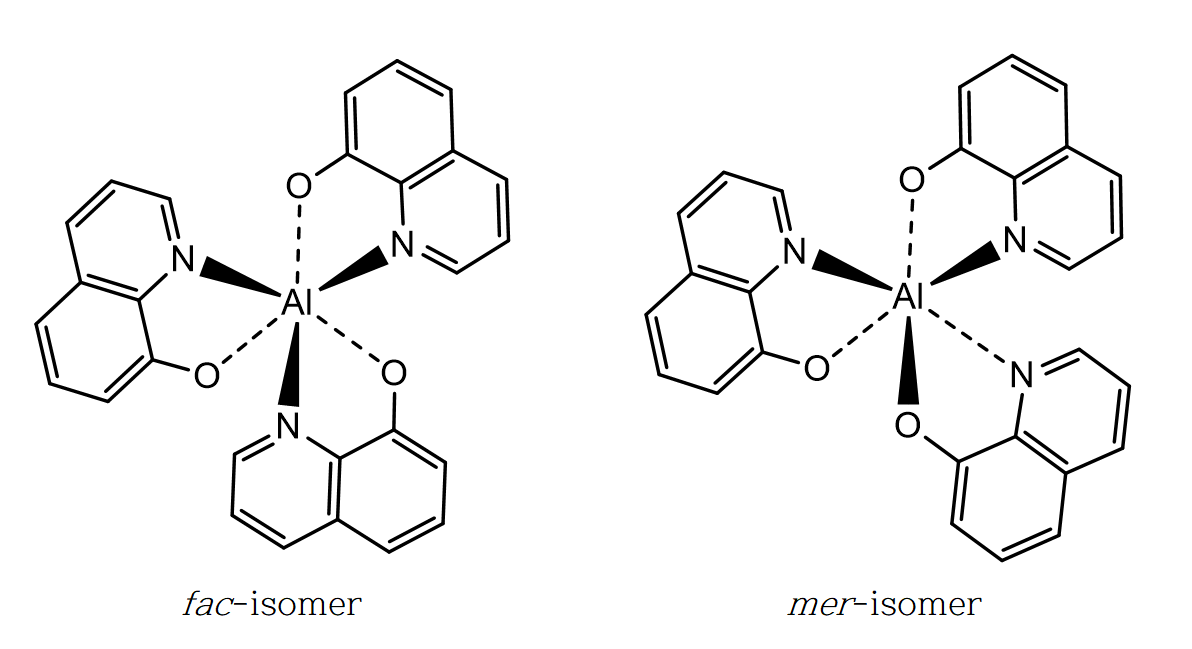
ㄱ. a는 2, b는 2 + 2 = 4 이므로, b/a = 2 이다. (참)

ㄴ. 두 착이온에서 금속 M의 산화수는 +2로 같다. (참)

ㄷ. 두 착이온 모두 facial, meridional 기하 이성질체를 갖는다. (참)

24번 답: ⑤ ㄱ, ㄷ

풀이:

표의 이온화 분율은 전체 농도 중에 [A^-], [B^-]가 차지하는 비율을 뜻한다. 용액의 부피를 공유하고 있으므로, 전체 몰수 중에 차이하는 A^- 또는 B^- 몰수라고도 할 수 있겠다. 작년부터 수능 화학2에서도 해당 개념을 이용하여 출제하고 있어서 유행인가 싶다. 이온화 분율로부터 짝산-짝염기 비율을 찾고, 헨더슨-하셀바흐 식을 이용하면, pH와 pK_a 등을 알 수 있는 유형의 문제다.

예를들어, 만약 전체 몰수가 1 mol이라면, pH = 4인 용액에서 생성된 A^- 몰수는 a mol이고, 남은 HA 몰수는 1 - a 이 된다. pH = 5 인 용액은 초기 몰수가 1 mol일 때, 생성된 A^- 몰수는 20a/11 mol이고, 남은 HA 몰수는 1- (20a/11) 이다.

HA의 용액의 pK_a는 주어진 pH에 무관하게 일정하므로, 헨더슨-하셀바흐 식을 통해 연립하면 a를 구할 수 있다. log와 분수 때문에 복잡해 보이지만, 직접 손으로 하다보면, 의외로 복잡하지는 않다.

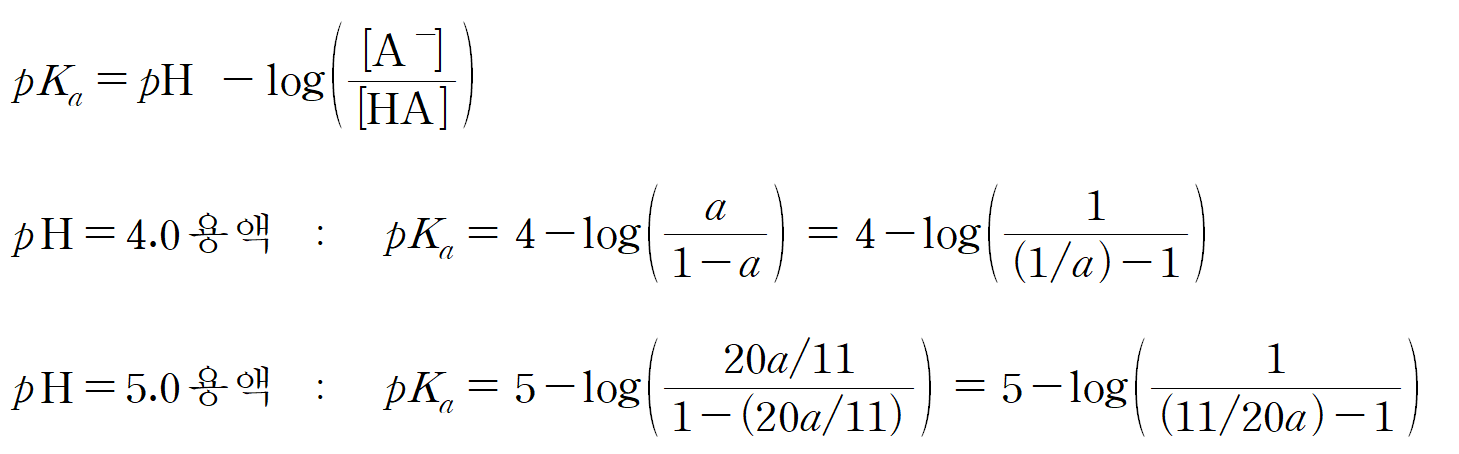
두 용액의 pK_a는 같으므로,

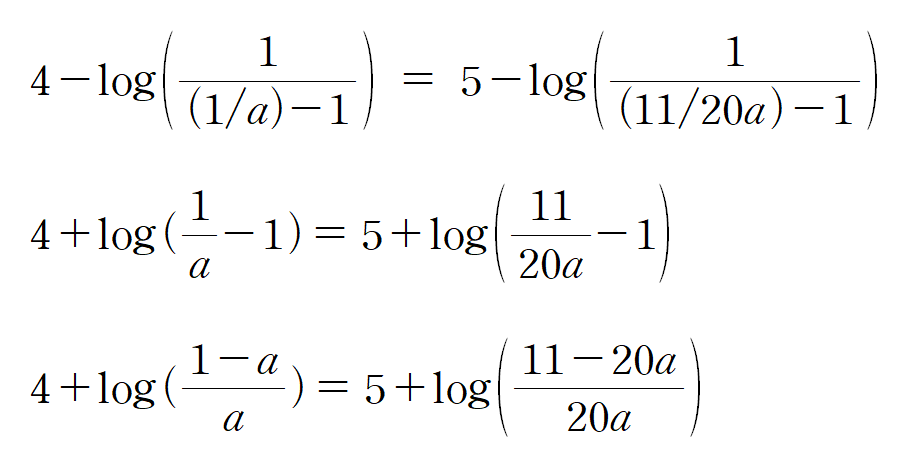
정리하면,

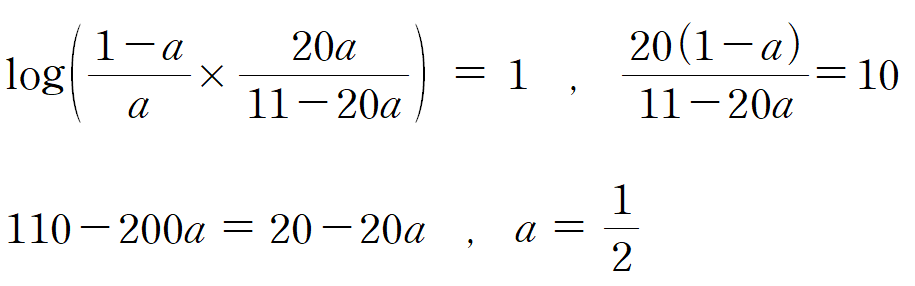
a = 1/2 , pH가 4인 HA의 용액의 [HA] = [A^-]이며, 약산 HA의 pK_a = 4임을 알 수 있다. a 값을 이용하여 HB의 pK_a를 구해보자.

pH = 5 인 HB 용액의 [B^-] 분율이 2a/11 이므로, 1/11이다. 이는 [HB] = 10 일 때, [B^-] = 1이라는 뜻이다. 짝산 : 짝염기 비율이 10 : 1이고, pH가 5이므로, 약산 HB의 pK_a = 6이다.

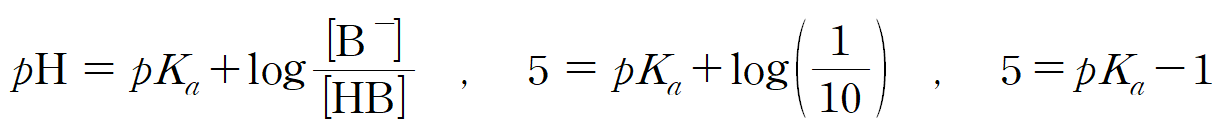
pK_a = 6인, HB 용액의 pH가 4라는 뜻은 짝산 : 짝염기 비율이 100 : 1 이라는 뜻이고, [B^-] 분율 b = 1/101이 된다.

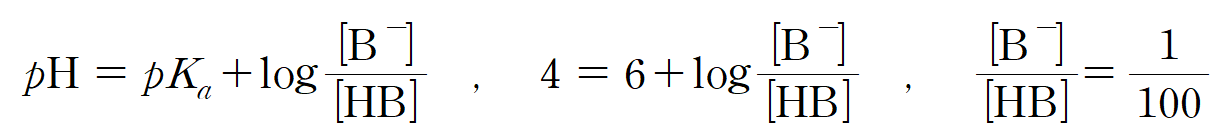
ㄱ. b/a = 2/101 이다. (참)

ㄴ. K_{a, HA} = 10^-4, HB의 K_{a, HB} = 10^-6 이므로, K_{a, HA} / K_{a, HB} = 10² = 100 이다. (거짓)

ㄷ. pK_a = 6인, HB 용액의 pH가 7이 되기 위해서는 짝산 : 짝염기 비율이 1 : 10이 되어야 하며, B^-의 분율은 10/11 = 20a/11 이 된다. (참)

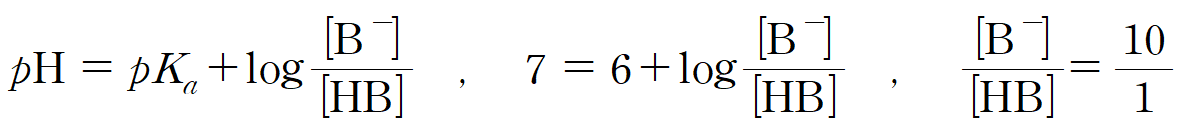
25번 답: ① ㄱ

풀이:

반응 (나)의 황(S)의 산화수 변화로부터 철(Fe)의 계수를 예측해보자. 초기 황의 산화수는 -2이며, 반응 후 황의 산화수는 +2이다. 황 하나당 산화수는 4만큼 증가했다. 전체 황의 개수가 6개이므로, 관여한 전자는 24개이다. 산화-환원은 언제나 짝지은 반응이므로, a개의 철이 환원되는데 관여한 전자도 24개이다.

철의 산화수는 +6에서 +3으로 변했으며, 철 하나당 산화수는 3만큼 감소했다. 따라서 철의 계수 a = 8이다.

a = 8을 대입한 후 반응 전후 전하 균형을 따져보면, 반응물 전하 합은 -28이며, 생성물의 전하 합은 - 6 - c 이다. 반응 전후 전하량은 같아야 하므로 -28 = -6 -c 이며, c = 22이다.

ㄱ. a = 8, c = 22 이므로, a + c = 30 이다. (참)

ㄴ. (나)에서 황의 산화수는 -2에서 +2로 4만큼 증가한다. (거짓)

ㄷ. 19,300초 동안 10 mA의 전류를 흘려보냈으며, 관여한 전자의 총 전하량은 193 C이다. 페러데이 상수 F = 96,500 C/mol이며, 이는 전자 1 mol의 해당하는 전하량(쿨롱, C)을 의미하므로, 반응에 관여한 전체 전자의 몰수는 193/96,500 = 0.002 mol = 2 mmol이다.

반응 (가)에서 철(Fe)의 산화수 변화는 +6이며, 1개의 금속 철이 산화되는데 관여하는 전자 또한 6 개이다. 전류를 흘려 관여한 전체 전자수가 2 mmol이었으므로, 산화된 철 원자는 1/3 mmol의 철 원자만 산화되었다. 생성된 FeO₄^2- 이온의 양 또한 1/3 = 10/30 mmol이다.

6개의 전자당 1개의 철이 산화 = 2 mmol 전자당 2/6 mmol개의 철이 산화

10/30 mmol이 존재하는 FeO₄^2- 용액에 가해진 S^2- 이온의 양은 0.005 M *20 mL = 1/10 = 3/30 mmol이다. 용액 내 FeO4^2-와 S^2- 존재하는 이온수 비는 10/30 : 3/30이지만, 반응은 8 : 6의 계수 비로 반응하므로, 한계 반응물은 S^2- 이다. 4 : 3 = x : 3/30 이며, 반응하여 Fe(OH)₂로 환원된 양은 x = 4/30 mmol 이다.

반응 (가)를 통해 생성된 FeO₄^2- 이온 10/30 mmol 중에 남은 양은 (10-4)/30 = 6/30 = 1/5 mmol이다. (거짓)

- 끝 -

* 본문 설명이나 풀이가 잘못된 부분에 대해 지적해주시면, 참고하여 수정·업데이트 하도록 하겠습니다. 위 문제의 출처는 http://www.kpeet.or.kr 한국약학교육협의회 사이트입니다.

728x90

저작자표시 비영리 변경금지