2024학년도 5월(5.8.) 고3 전국연합학력평가 화학2 풀이 [3점 문항]
2024학년도 5월(5.8.) 고3 전국연합학력평가 화학2 풀이 [3점 문항]
지난 수요일(5.8.)에 시행된 경기도교육청 주관 고3 전국연합학력평가의 화학2 3점 문항 풀이를 남겨둔다. 3점 문항은 5번, 8번, 10번, 11번, 12번, 13번, 16번, 18번, 19번, 20번으로 총 10문항이다. 문제지와 공식 해설지는 모두 EBSi 사이트에서 다운로드 받을 수 있다. 화학2 선택자 수가 거의 소멸 직전이기에 해당 풀이를 찾아보는 이가 없겠지만, (혹시나) 혼자 외로운 싸움을 하는 학생들이 있다면, 아주 조금이나마 도움이 되었으면 한다.
이번 학력평가는 5월에 시행되었기에 출제 범위가 다소 좁았다.
출제 범위는 따로 찾아보지 않아 확실치 않지만, 평형 상수와 평형 이동까지에 해당하는 것으로 보이며, 산-염기 평형과, 상평형, 화학 반응 속도론, 전기 화학 등은 출제되지 않았다. 시험 당시에 화학2 진도가 반응 엔탈피 직전까지였는데, 우리 학교 학생들 입장에서는 쉬운 문제 다수를 미처 배우기 전이라 풀 수 없어 다소 아쉬웠을 수 있었겠다. (물론 선택을 하는게 먼저겠지만,,,)
(PC환경에서) Ctrl + F 검색에서 "00번" 으로 검색하면, 원하는 문제로 쉽게 화면 이동할 수 있습니다.

5번 정답 : ④ ㄴ, ㄷ
풀이 :
삼투압은 반투막에 의해 분리된 두 용액의 농도 차이가 클수록 크고, 용액의 온도가 높아질수록 커진다. 문제 조건에서 온도가 일정하므로, 용액의 농도 차이가 클수록 삼투압에 의한 수면의 높이 차이가 커진다.
ㄱ. 반투막은 비교적 큰 용질은 통과하지 못하고, 용매인 물만 통과시킬 수 있는 선택적 투과성을 갖는다. 압력 평형을 이룬 과정 (나)에서도 물은 여전히 반투막을 통과하며, 지속적으로 이동한다. (거짓)
ㄴ. 용매의 이동은 저농도 → 고농도 방향이며, 물의 이동이 많아질수록(삼투압이 커질수록) I과 II의 수면 높이 차이가 심해진다. 물이 흘러들어오는 II의 수면 높이가 I에 비해 높다. (참)
ㄷ. 수용액의 농도가 증가했으므로, 삼투압 역시 증가하고, 삼투압에 의한 높이 차이(h2)는 기존 차이(h1) 보다 더 커진다. (참)
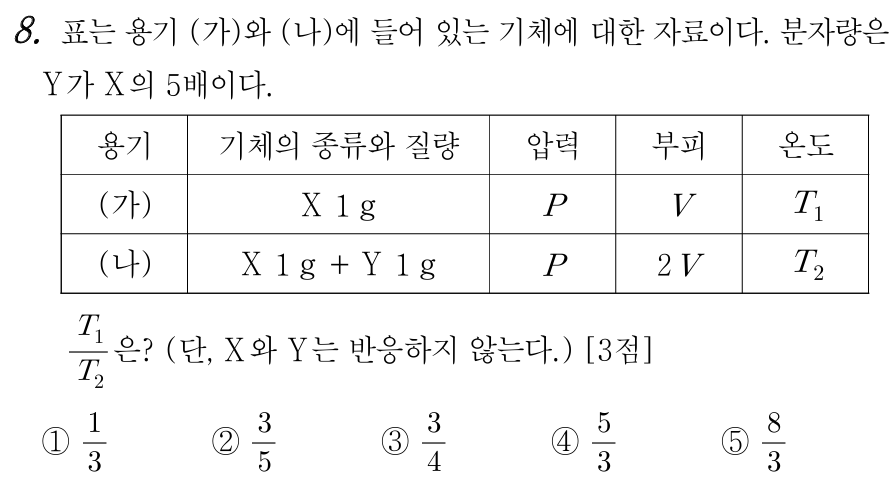
8번 정답 : ② 3/5
풀이 :
문제 조건에서 분자량이 Y = 5X 라고 주어져 있으므로, Y의 분자량 = 5, X 분자량 = 1 이라 하면, (가)는 X 1 mol 이, (나)는 X 1 mol + Y 0.2 mol이 존재한다. (가)는 전체 1 mol, (나)는 전체 1.2 mol 이다.
문제에서는 T1/T2를 묻고 있으며, 이는 이상기체 방정식을 통해 비교할 수 있다. PV = nRT 이며, T = PV/nR 이다. (가)와 (나)에서 P와 기체 상수 R은 동일하므로, 상수 취급하고, T ∝ V/n 에 의존하는 것을 알 수 있다.
(가)의 T1 ∝ V/1 이며, (나)의 T2 ∝ 2V/1.2 이다. T1/T2 = 1.2/2 이므로, 3/5이다.

10번 정답 : ④ ㄱ, ㄷ
풀이 :
결국 용액 (다)는 (가)와 (나)의 용질, 용액으로 이루어지며, 혼합 전후 질량은 일정하다. 화학2에서의 농도 환산은 대부분 몰랄농도가 중심이 되며, 변환 과정에서 질량 농도 분율(w/w)로 바꾸어 생각하면, 수월한 경우가 많다.
ㄱ. (가)는 0.6 M 용액 1 L 이므로, 용질은 0.6 mol = 60 g, 용액은 1 L * 1040 [g/L] = 1040 g 이다. 자연스레 물의 질량은 1040 - 60 = 980 g 이다. (참)
ㄴ. (나)는 몰랄 농도가 0.5 m이다. 용질이 0.5 mol = 50 g일 때, 용매는 1 kg = 1000 g 이라는 뜻이다. 즉, 50 g의 용질이 용액 1050 g에 녹아 있다. 그런데 (나) 용액의 전체 질량은 126 g이다. 126 g 속에 녹아 있는 용질의 양은 다음과 같이 구할 수 있다. (거짓)
[ 50 g(용질) / 1050 g(용액) ] * 126 g(용액) = 6 g(용질)
ㄷ. (가)와 (나)를 혼합한 (다)에는 용질 60 + 6 = 66 g이, 용매 980 + 120 = 1100 g 으로 구성된다. 몰랄 농도에 맞춰 생각해보면, 용질 66 g = 0.66 mol, 용매 1100 g = 1.1 kg 이므로, x = 0.6 이다. (참)

11번 정답 : ② 60
풀이 :
순수한 물의 증기압은 62 mmHg, 용액의 증기압은 60 mmHg이므로, 용액 내 X물 = 60/62 = 30/31 이다. 즉, 이 용액은 물 30 mol과 A 1 mol에 의해 구성된 용액이라는 뜻이다.
물(용매) 30 mol = 30 * 18 = 540 g 이고, A(용질) 1 mol = 분자량 X g 이므로, 다음을 만족한다.
X / (540+X) = 1/10 , (540/X) + 1 = 10 , 따라서 X = 60 이다.

12번 정답 : ③ ㄱ, ㄷ
풀이 :
ㄱ. C3H8 (g)의 생성 엔탈피에 해당하는 것은 ΔH1 이다. 생성 엔탈피는 생성물 1 몰이 가장 안정한 홑원소물질로부터 생성되는 과정에서의 엔탈피 변화이다. ΔH1에 해당하는 반응은 생성물의 엔탈피가 반응물의 엔탈피 합보다 작다. (ΔH1 < 0) (참)
ㄴ. ΔH3은 흑연 3 mol이 완전 연소할 때의 반응 엔탈피이다. 따라서 흑연 1 mol이 완전 연소할 때의 반응 엔탈피는 ΔH3/3 이다. (거짓)
ㄷ. ΔH2 = ΔH1 역반응 → ΔH3 → ΔH4 경로를 거쳐도 똑같이 구할 수 있다. 따라서 ΔH2 = - ΔH1 + ΔH3 + ΔH4 이다. (참)
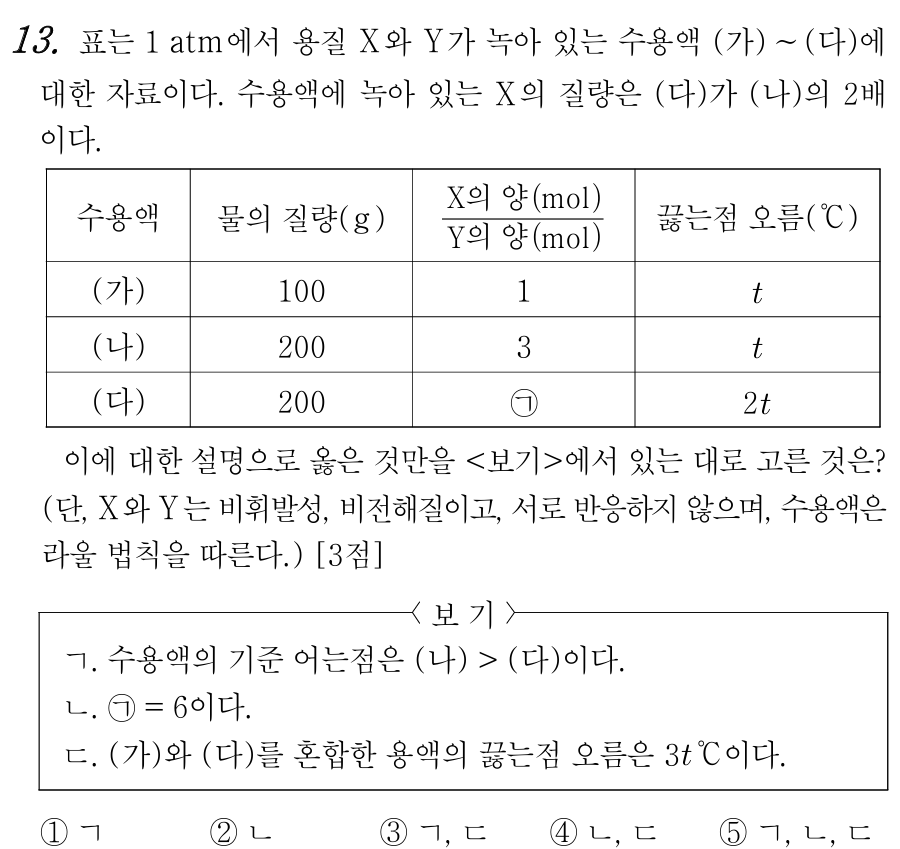
13번 정답 : ① ㄱ
풀이 :
(가)와 (나)의 끓는점 오름이 같다. 같은 수용액이므로 Kb(몰랄 오름 상수)는 같으며, 두 용액의 몰랄 농도(m)도 같다. 물의 질량이 (나)가 (가)의 2배이므로, (나)의 용질 몰수가 (가)의 2배이어야 두 용액의 몰랄 농도가 같아진다.
(가)와 (나)에서 X/Y 값이 1과 3이므로, (나) 용액에 포함된 X = 3 mol, Y = 1 mol, 전체 = 4 mol 이라고 하면, (가) 용액에 포함된 X = 1 mol, Y = 1 mol, 전체 = 2 mol이 된다.
(다)의 끓는점 오름은 (나)의 2배이므로, (다)의 몰랄농도는 (나)의 2배임을 알 수 있다. (나)와 (다)의 용매 질량이 같으므로, (다)에 포함된 전체 용질 = 8 mol이 된다.
제시 조건에서 (나)보다 2배 많은 X가 (다)에 포함되어 있다고 했으므로, (다)의 X = 6 mol 이고, 자연스레 Y = 8 - 6 = 2 mol이 된다.
ㄱ. 몰랄농도가 더 큰 (다) 용액의 어는점 내림이 더 심하다. 따라서 기준 어는점은 (다) < (나)이다. (참)
ㄴ. (ㄱ) = 6/2 = 3 이다. (거짓)
ㄷ. (가)와 (다)를 혼합한 용액의 몰랄 농도는 10/0.3 = 100/3 이다. (가)를 통해 2/0.1 = 20 일 때, 끓는점이 t ℃ 상승하므로, 혼합 용액의 끓는점은 (100*t)/(3*20) = 5t/3 ℃ 상승한다. (거짓)
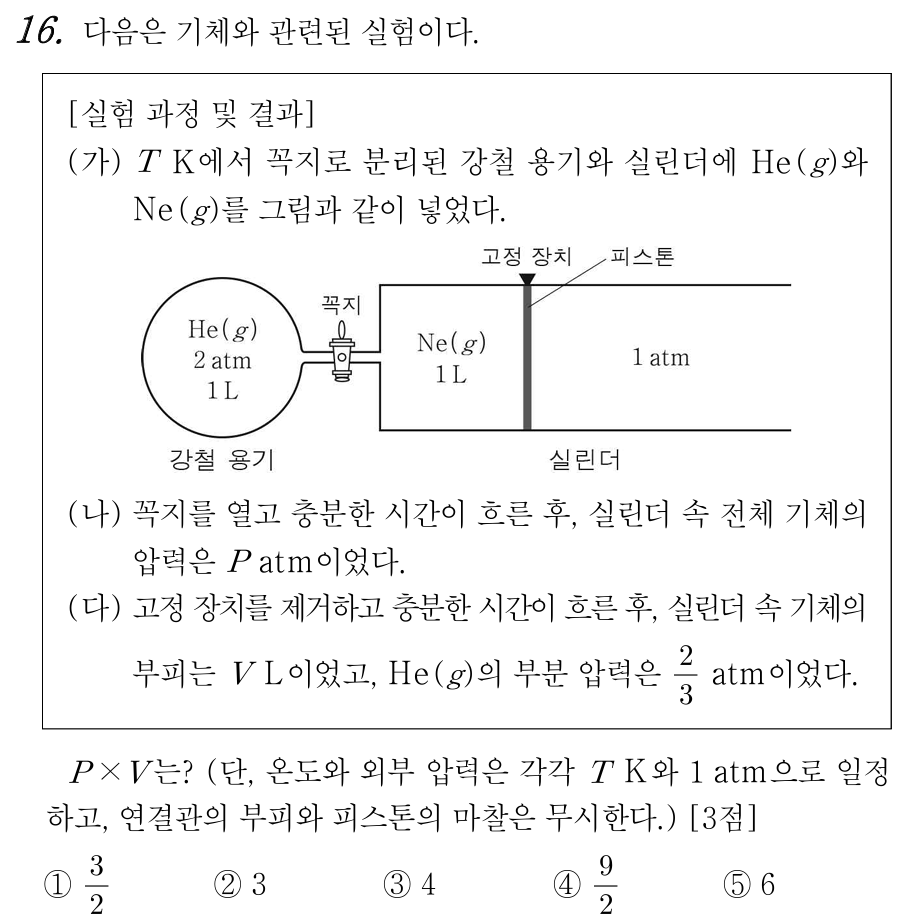
16번 정답 : ② 3
풀이 :
과정 (나)에서 꼭지를 열고, (다)에서 고정 장치를 풀면, 혼합 기체 전체 압력은 외부압과 평형을 이루고 1 atm이 된다.
과정 (다) 이후 He 부분 압력이 2/3 atm 이라는 것은, 전체 압력이 1 atm인 상황이므로, He 몰분율이 2/3이라는 뜻이며, 나머지 기체인 Ne 몰분율이 1/3이라는 뜻이다. 이에
초기 He의 몰수 = 2 atm * 1 L = 2 mol이라 하면, 초기 Ne의 몰수 = 1 mol = 1 atm * 1 L 라고 할 수 있다.
과정 (나)에서 꼭지만 열었을 때, 전체 3 mol의 기체가 고정된 피스톤에 의해 2 L 공간에 퍼져 있으므로,
혼합 기체의 P atm * 2 L = 3 mol , P = 1.5 atm 이 된다.
이 상태에서 (다)의 고정 장치를 풀면 전체 기체 압력은 1 atm이 되며, 1 atm * (1+V) L = 3 mol 이 되므로, V = 2가 된다.

18번 정답 : ④ 3/8
풀이 :
위의 문제 상황에서 두 가지가 사실은 변하지 않는다. 일정 온도에서 기체의 압력과 부피의 곱(PV )은 몰수와 같이 생각할 수 있고, 피스톤으로 구분된 두 공간은 서로 압력 평형을 이룬다.
세 구역으로 분리된 (가)의 초기 상태에서 강철 용기의 A는 2 mol, 실린더 I의 B는 1 mol, 실린더 II의 B는 2 mol 존재한다. 과정 (나)에서 꼭지 a를 열면, 강철 용기의 A와 실린더 I의 B가 반응을 하며, 한계 반응물은 B이다. B 1 mol이 모두 소진되고, A는 2 - 0.5 = 1.5 mol이 남고, C가 생성된다.
꼭지 a를 열고, 반응이 충분히 진행되었음에도 실린더 I의 부피가 변하지 않고, 여전히 1 L라는 것은 전체 압력이 1 atm으로 유지되고 있음을 뜻한다. 그리고 강철용기와 실린더 I 내에 포함된 전체 기체(A+C)의 양이 2 mol이라는 것을 뜻한다. 생성된 C는 0.5 mol이고, 반응 비에 따라 계수 c = 1 이다.
(다)에서 꼭지 b를 열면, 남은 A 1.5 mol과 B 2 mol이 반응하며, 계수 비에 따라 한계 반응물은 B이다. A는 1.5 - 1 = 0.5 mol 남고, 이 반응을 통해 C는 1 mol 생겨난다.
최종적으로 남아있는 기체는 A 0.5 mol과 C 0.5+1 = 1.5 mol 이며, 전체 기체(A+C) 몰수는 2 mol이다.
2 mol의 기체가 총 4 L의 공간에 퍼져있으므로, 전체 기체의 압력은 1/2이며, 이 중 C의 부분압력 P = 전체 압력*몰분율 = (1/2) * (3/4) = 3/8 이다.

19번 정답 : ① (2a - x)/2
풀이 :
모든 결합을 고려하지 않고 OF2가 O2와 반응하여 O2F2가 되는 과정에서 끊어져야 하는 결합과 새로 생겨나는 결합 관계만 생각해주면 된다. (문제에서 따로 O-F 결합 에너지에 대한 정보를 주지 않은 이유도 이를 바탕으로 한다.)
2 mol의 F-O-F 이 반응하여 2 mol의 F-O-O-F 이 될 때, 2 mol의 O-O 결합이 새롭게 생겨난다. O-O의 결합 에너지를 y라 한다면, 2 mol의 O-O 결합이 생성되는 반응의 엔탈피 변화는 -2y가 된다.
그리고, 1 mol의 O=O 결합이 끊어져야 한다. (½O2 → O 의 반응 엔탈피(O의 생성 엔탈피)가 a 이므로, O=O의 결합 에너지는 2a 이다.
즉, 위 반응식의 반응 엔탈피 x는 1 mol의 O=O 결합을 끊고, 2 mol의 O-O 결합이 생성되는 과정이므로, x = 2a -2y 이다. 문제에서 요구하는 y = (2a - x) / 2 이다.

20번 정답 : ⑤ ㄱ, ㄴ, ㄷ
풀이 :
(가) → (나)에서 반응한 A = 1/4 mol이다. 반응식의 계수비에 따라 생성된 B = 2/4 mol 임을 알 수 있다. (나)에서 기체 전체의 몰수는 (3/4) + (2/4) = 5/4 mol이다.
(나)에서 온도를 변화시켜서 새로운 평형 상태에 도달했을 때, A와 B의 질량이 같았다. 화학 반응식이 A → 2B 이므로, A의 분자량은 B의 2배이다. A, B의 질량이 같다면, B의 몰수가 A의 2배라는 뜻이다.
ㄱ. 새로운 평형에서 A와 B의 몰수는 A = (3/4) - x mol, B = (2/4) + 2x mol 이며, A와 B의 질량 관계(몰수 관계)를 바탕으로 찾아낸 몰수 관계에 따라 (3/4 - x)*2 = (2/4 + 2x) 이므로, 4x = 1 이고, x = 1/4 이다.
즉, (다)에서 A = 2/4 mol , B = 1 mol 이다. (참)
ㄴ. (나)와 (다)의 몰수와 부피를 바탕으로 평형 상수 K 값을 구할 수 있다. (나)의 평형상수 K = (1/2V)2 / (3/4V) = 1/3V 이고, (다)의 평형상수 K ' = (1/2V)2 / (1/4V) = 1/V 이다. 따라서 K '/K = 3 이다. (참)
ㄷ. 온도를 변화시켰는데, V는 2배 증가했으며, 전체 입자수는 (나) : (다) = 5 : 6 이다. 일정 압력에서 T ∝ V/n에 비례하므로, T1 : T2 = 1/5 : 2/6 = 6 : 10 이다. T2의 온도를 높였을 때, 평형 상수가 증가하고, 정반응이 우세하게 진행되었으므로, 위 반응은 ΔH > 0인 흡열 반응 이다. (참)
- 끝 -
* 위 연합학력평가의 주관교육청은 경기도교육청이며, 문제와 정답(해설)은 EBSi 홈페이지에서 확인할 수 있습니다.