상자 속 입자 (The Particle in a Box, PIB)
상자 속 입자 ( The Particle in a Box, PIB)
어쩌다가, 입자는 상자에 빠지게 되었나...
0. 들어가기
수업을 구성할 때, 전반적인 흐름에 가장 신경을 쓰는 편이다. 이 단원이 왜 가장 먼저 등장하는지, 이런 요소들이 왜 함께 묶여 있는지, 뜬금없이 왜 이러한 탐구 활동이 나오고, 왜 이런 유형의 문제를 풀고 연습해야 하는지에 대해 학생들을 이해시키고자 한다. 그러다 보니 항상 도입부에서 혀가 길다.
같은 이유로, 수업을 준비하는 과정에서 도입 부분이 마음에 들지 않으면 진척이 되지 않는 면도 있다. 여러 이유가 복합적으로 얽혀서 만들어진 결과이겠지만, 과거의 내가 학습하는 과정 중에 학습 내용이 어디에 연결되고 어떤 흐름 속에서 등장하게 된 것인지를 끊임 없이 묻고, 그 질문에 대한 답을 찾기 위해 많은 시간을 보냈기에 현재의 내가 그런 것들에 집착하는 것일 수도 있겠다고 개인적으로 생각한다.
-
대학 화학에서 처음 접하게 되는 것들이 있다. 당장 생각나는 것으로는 슈뢰딩거 파동 방정식과 파동 함수, 분자 오비탈, 전이금속화학, 침전 평형 등이 있는데, 고등학교 화학1, 2 연장선에 있어서 흐름상 큰 문제가 되지 않는 것도 있지만, 완전히 새롭게 시작해야 것(분자 오비탈, 전이금속화학)들도 있다. 교육 과정이 바뀜에 따라 고교 화학 내용 요소가 점차 쪼그라드는 경향 속에서, 어찌 되었건 빠짐없이 정해진 양을 가르치고, 배워야 하는 대학에서의 어려움이 점점 커지는 것도 분명해 보인다.
아주 오래 전이지만, 대학에서 양자역학 도입부에서 상자 속 입자를 처음 접했을 순간을 잊을 수 없다.
뜬금없이 알맹이가 상자에 갇히고, 상자에 갇힌 입자의 에너지가 왜 궁금한지, 그걸 구해야 하는 이유도 잘 모르겠는데, 별로 사이가 좋지 않은 sin, cos, 적분 등이 등장하며 칠판이 점점 유도 과정으로 채워지고, 나는 그저 이해할 노력 없이 옮겨 적기에 급급 했었다. (결국, 미래의 나에게 필기를 남겼지만...)
이번 글을 통해서는 대부분은 일반 물리학(또는 고등학교 고급 물리)에서 처음 접하고, 화학을 하더라도 일반화학의 양자역학 관련 단원 도입에서 소개되는 상자 속 입자에 대해 이야기 해보고자 한다.
1. 입자는 어쩌다 상자에 빠졌나?
상자 속 입자는 일종의 모형(model)이다. 비유이며, 자연 현상을 설명하기 위한 일종의 상황극과 같다. 기체 분자 운동론에서는 눈에 보이지 않는 기체 입자들이 어떠한 방식으로 운동하는지 설명하기 위해 상자 안에 기체 입자를 가두고, 슈뢰딩거는 닐스 보어가 주장한 양자 역학의 불완전성을 지적하기 위해 독극물과 함께 고양이를 상자 속에 가두었다. (물론, 머릿속으로만...)

상자 속 입자 모형도 이러한 비유로 생각하면 좋다.
높이가 무한대인 절대로 빠져나올 수 없는 상자에 입자 하나가 빠졌다. 무한대 깊이의 우물이라고 표현해도 괜찮다. 어차피 무한대의 높이여서 뚜껑이 막힌 상자인지, 열린 우물인지는 상관이 없다. 입자가 어떤 짓을 해도, 못 빠져나오는 상황이 설정되었음이 중요하다.
과학자들은 무언가 가두고 구속하는 것을 좋아하는가?라고 생각할 수 있지만, 상자 속 입자에서는 복잡해질 수 있는 요소를 사전에 통제하여 간단한 상황 설정을 위해 가뒀다. (입자야... 너도 좀 잘 살펴보고, 좀 조심하지 어쩌다가 거길 빠지냐...)
상자 속에 입자가 빠진 상황으로 무엇을 설명할 수 있을까? 바로, 원자 상태이다. 상자 속 입자는 전자를 뜻하고, 상자 속에 빠져있는 상황 자체가 전자가 핵에 붙들려 만들어진 원자 모습을 말한다. 그렇다면, 상자 높이가 무한대로 설정되어 입자가 빠져나올 수 없다(무한 퍼텐셜 우물)는 조건도 전자가 핵을 벗어나 독립적으로 탈출한(이온화) 상태는 여기서 다루지 않겠다는 것임을 눈치챌 수 있다.
정리하자면, 상자 속 입자는 전자와 핵의 상호작용을 통해 만들어지는 원자 상태에서의 전자를 설명하고 이해해 보기 위한 모형이라 할 수 있겠다.
2. 상자 속 입자로 원자 구조 이해하기
상자 속에 갇힌 입자는 곧, 핵에게 붙들린 전자가 갖는 특성을 설명한다. 전자는 원자 내에서 자유롭게 존재할 수 있지만, 존재할 수 있는 공간은 핵의 영향력이 닿는 영역으로 제한된다. 전자는 원자 내부에서 어디에든 존재할 수 있을까? 전자가 존재할 확률은 위치와 무관하게 모두 같을까?
고전역학에서는 입자에 작용하는 모든 힘, 입자의 초기 위치, 초기 속도가 주어지면 입자의 미래를 정확하게 예측할 수 있었지만, 양자역학 세계에서는 그렇지 않다. 어떤 위치(지점)에서 입자가 발견될 확률만 알 수 있다.
즉, 고전 역학에서는 상자 속에 갇힌 입자에 어떤 힘이 작용하고 어떤 운동을 하는지 알면, 특정 순간에 입자가 어디에 있을지 정확하게 예측 가능했지만, 양자역학에서는 그 위치(지점)에서 발견될 수 있는 확률만 알 수 있다는 뜻이다.
이제, 상자 속에 입자를 빠뜨려 보자.
-
길이가 L인 1차원 상자에 질량이 m 인 입자가 빠졌다. 핵에 붙들린 전자 상황이므로, 입자가 상자 밖으로 빠져나가면 안 된다. 따라서, 상자 높이(입자가 뛰어넘어야 하는 퍼텐셜 장벽)는 ∞ 로 설정한다. 이제 제 아무리 전자가 빠르고 날쌔도, 발판을 밟고 점프하여 밖으로 나가려 안간 힘을 써도 벗어날 방법은 없다.

1) 경계 조건 (Boundary Condition)
무한 퍼텐셜 장벽을 설정한 덕분에 상자 밖에서는 입자가 발견될 수 없다. 따라서 위의 상자 밖 x < 0 , x > L 구간에서는 입자가 존재하지 않으며, 입자의 파동함수(ψ(x))도 0이다.
x = 0 , x = L 지점은 상자 안과 밖을 구분 지어주는 경계 지점이다. 상자 내부 입자의 파동함수(ψ(x))는 상자 밖에서도 연속적인 함수로 표현되어야 하는데, 상자 밖에서의 ψ(x) 값이 0 이므로, 경계가 되는 x = 0, x = L 지점에서의 ψ(x) 값은 0이 되어야 연속적일 수 있다. 이를 경계 조건(Boundary condition)이라 한다. 종합하면,

2) 상자 속 입자의 파동 함수
이제, 상자 내부를 보자. 상자 속 입자의 에너지는 운동 에너지와 퍼텐셜 에너지를 모두 따져주어야 하겠지만, 처음부터 복잡할 필요는 없으니, 퍼텐셜 에너지(V(x))는 없다고 가정하자. 상자 속 입자가 만족하는 파동 방정식(Ηψ = Εψ)은 다음과 같이 간단해지고, 이를 통해 얻어지는 에너지 E 는 오직 입자의 운동 에너지로만 생각할 수 있다.

상자에 갇힌 입자의 파동 함수(ψ)는 어떠한 형태를 가질까? 어쨌든 파동이니까 sin과 cos의 조합으로 표현될 것 같은데, 처음부터 알 수 없으니 일반화된 식의 형태로 시작해 보자.

상자 속 입자의 파동 함수는 경계 조건을 만족해야 하므로, [1] ψ(0) = 0이고, [2] ψ(L) = 0을 만족해야 한다.
[1] 일단, 경계 조건의 x = 0을 먼저 대입해 보면, ψ(0) = 0 이 되어야 하므로, B cos 0 + A sin 0 = 0 이며, B 는 반드시 0이 되어야 한다.
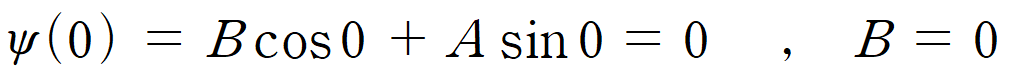
이제, 파동 함수 ψ(x)는 이전보다 간단한 형태가 되었다.
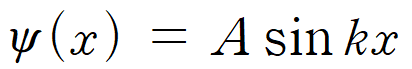
[2] 남아 있는 나머지 경계 조건을 적용시켜 보자. x = L을 대입하면, ψ(L) = 0 이어야 하므로, A sin kL = 0 을 만족해야 한다. sin 함수가 0이 되기 위해서는 kL 값이 π, 2π, 3π … 을 만족해야 한다.
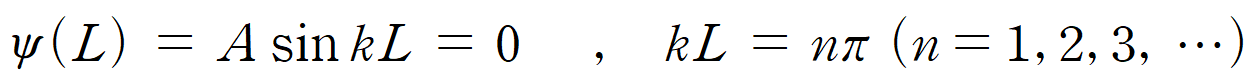
이제 상자 속 입자의 파동 함수식은 더 간단한 형태로 나타낼 수 있게 되었다. (k = nπ/L 이므로)
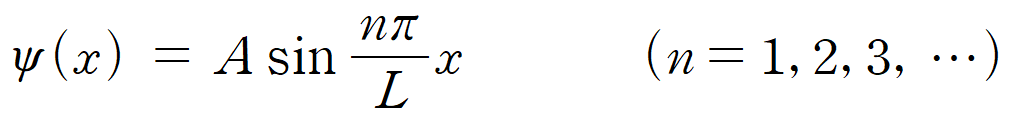
거의 다 되었지만, 아직 결정되지 않은 것이 있다. 계수 A이다. 마지막 A는 정규화(normalization) 조건을 적용하여 결정할 수 있다.
3) 정규화(normalization)
슈뢰딩거의 파동 방정식(Ηψ = Εψ )을 풀면, 전자의 파동 함수 ψ 를 구할 수 있으며, 파동 방정식의 해인 파동 함수 ψ 는 전자에 관한 모든 정보를 담고 있다고 할 수 있다. 독일의 물리학자 막스 보른(Max Born, 1882-1970)은 "전자의 파동 함수를 제곱한 것(ψ2)을 전자를 발견할 단위 부피당 확률"로 해석할 수 있음을 말했다. 우리는 ψ2 을 확률 밀도(probability density)라 부른다.
이 개념을 상자 속 입자로 가져와보자.
상자 속 입자의 파동 함수(ψ )를 제곱하면, 상자 속 공간에서 입자를 발견할 확률에 대해 알 수 있다. x축 1차원 상자이므로, ψ2(x) dx는 x 에서 dx 사이 미소한 구간에서 그 입자를 발견할 확률에 비례한다. 어떤 지점 또는 구간의 ψ2(x) 값이 크다는 것은 그 지점 또는 구간에서 입자를 발견하기 쉽다는 뜻이다.
파동함수 제곱이 확률로 해석될 수 있다면, 결국 상자 속 각각의 지점(x)에서 입자가 존재할 확률을 모두 더하면 1이 되어야 한다는 뜻이다. 상자 길이가 L 이므로, 0 에서부터 L 사이 구간에서 전자를 발견할 확률(ψ2)의 적분 값은 1이 되어야 한다.
이러한 조건을 만족할 때, 파동 함수는 정규화(또는 규격화, normalization)되었다고 할 수 있다.
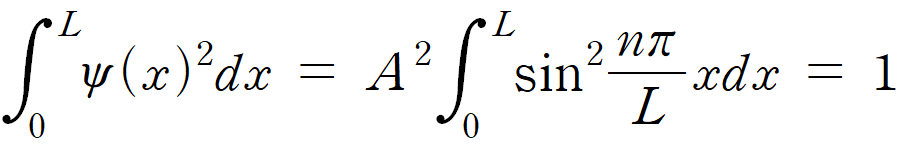
ψ 를 제곱했을 때, 나타나는 sin2x 형태를 적분하기 위해서는 이중각 공식을 이용하여 [1 - cos(2x)]/2 형태로 변형해야 한다. 여기는 수학 영역인 것 같으니 은근슬쩍 넘어가자. 다음과 같이 식을 변형할 수 있다.
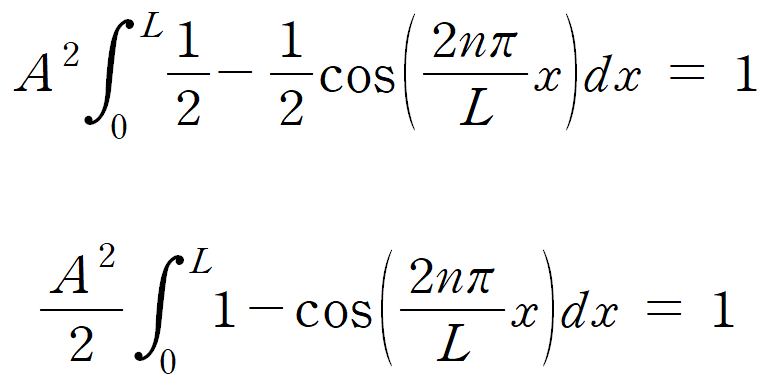
[참고] 작성자는 설명할 수 없는 삼각함수의 이중각 공식
0부터 L 까지의 구간에 대해 적분하면, 이를 만족하는 A의 값을 얻을 수 있다. A = (2/L)1/2 이다.
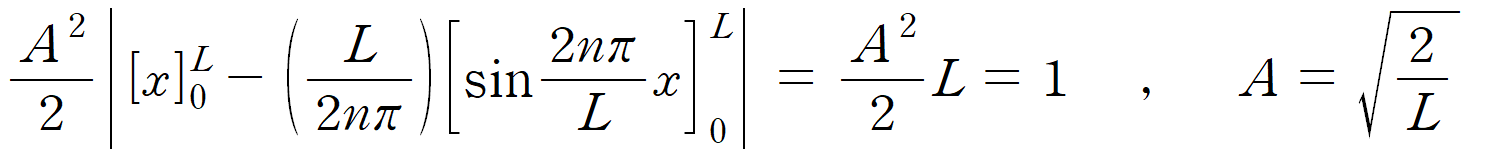
드디어, 길이가 L인 상자 속에 갇힌 입자의 파동 함수 식(ψ(x))을 완전히 알아냈다.
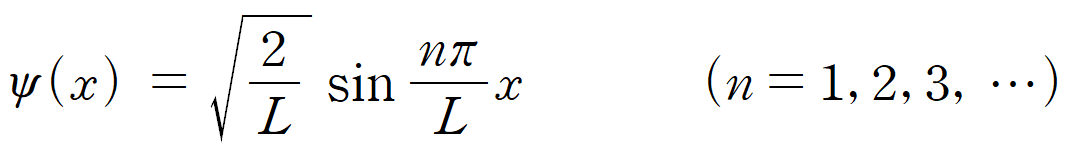
3. 상자 속 입자의 에너지
길이가 L 인 1차원 상자 속 입자의 파동 함수를 찾았다. 이 파동 함수 ψ는 파동 방정식 ΗΨ = ΕΨ 의 해가 된다. 파동 함수와 파동 방정식을 이용하면, 상자 속에 갇힌 입자의 에너지(E )에 대한 정보를 얻을 수 있다. (참고로, 드 브로이 식과 고전적인 운동에너지 식만을 이용하여 같은 결과를 보여줄 수도 있다.)
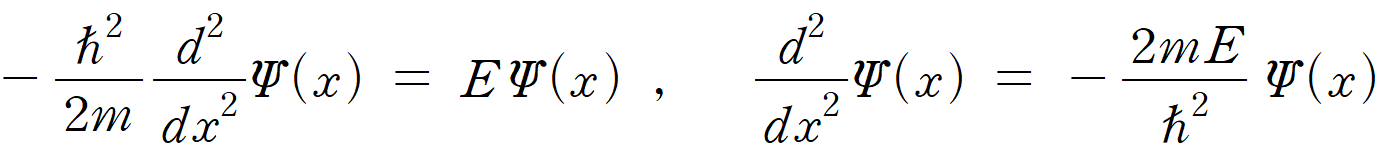
결과만 살펴보면, 좌변의 파동 함수 ψ(x)를 x에 대해 두 번 미분한 2차 도함수 ψ''(x)와 - 2mE / (hbar)2에 파동 함수 ψ(x)를 곱한 결과가 같다는 것이다. 위에서 찾은 상자 속 입자의 파동 함수를 연달아 미분해보면,
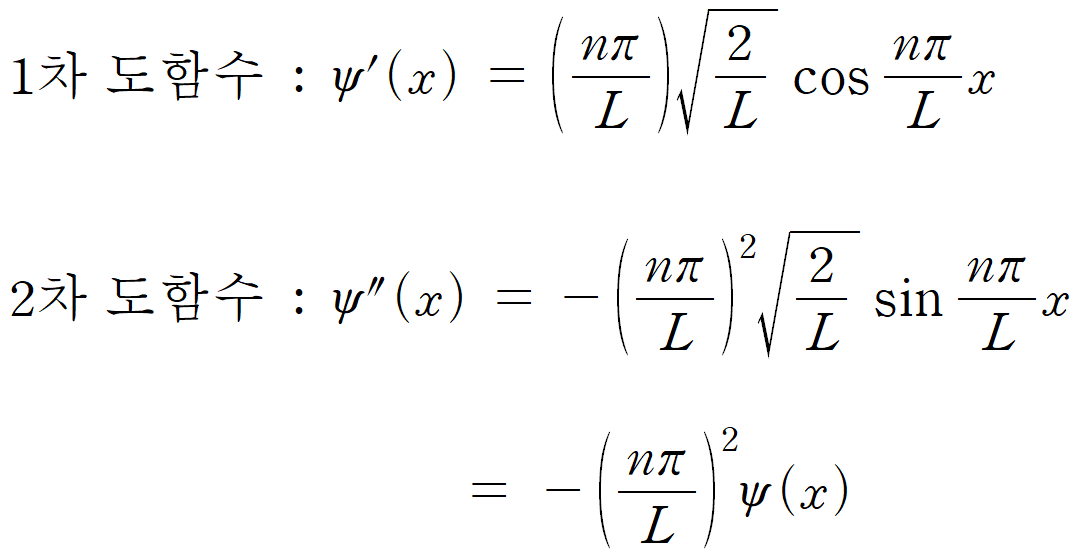
결국, 2차 도함수의 -(nπ/L)2 이 - 2mE / [(hbar)2]와 같아야 한다. 그리고, 이러한 과정 속에서 알 수 있는 상자 속 입자의 에너지 E 는 다음과 같다.
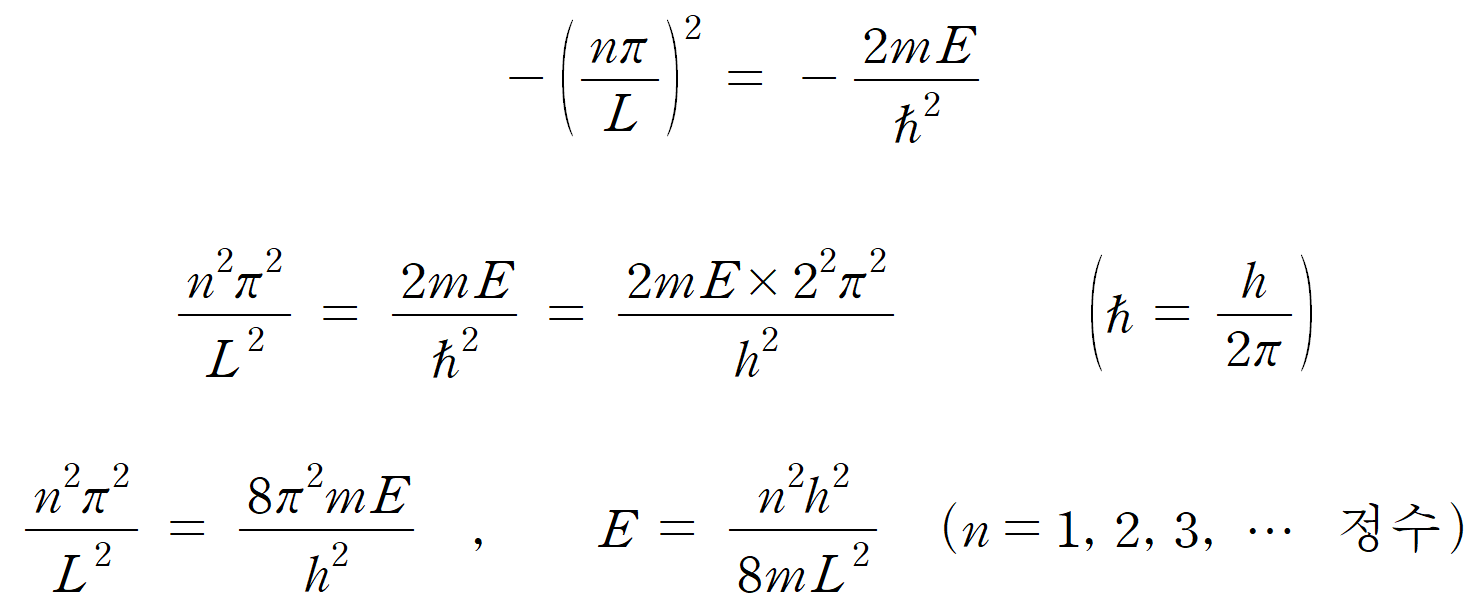
이것이 뜻하는 바가 무엇일까?
가장 먼저 눈에 띄는 것은 상자 속에 갇힌 입자의 에너지가 양자화되어 있다는 사실이다. 에너지 식의 n = 1, 2, 3 … 등의 정수 값만을 가지며, 결과 또한 특정 값만을 갖게 된다. 이는 핵에게 붙들린 전자의 에너지가 연속적이지 않고 양자화되어 있음을 뜻하며, 각 에너지 준위의 간격(ΔE ) 또한 불연속적이라는 것을 보여준다.

또한, 상자 속에 갇힌 입자가 가질 수 있는 가장 작은 에너지는 n = 1 일 때인데, E1 = h2/8mL2 의 값을 갖는다. 이 때의 에너지를 영점 에너지(zero-point energy)라 하며, 상자 속 입자는 0이라는 에너지 값을 가질 수 없고, 어떤 최소한의 에너지 값을 가짐을 알려준다.
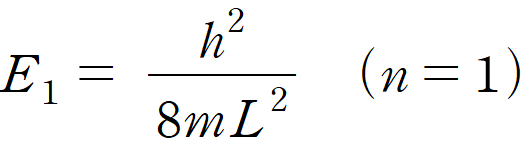
- 끝 -
* 끝까지 읽어주셔서 감사합니다.
[다음 글]
334. 상자의 길이 변화로 설명하는 물질의 색(feat. 짝불포화계) https://stachemi.tistory.com/334
상자 길이 변화로 설명하는 물질의 색(feat. 짝불포화계)
이전 글 : 1차원 상자 속 입자 https://stachemi.tistory.com/327 상자 속 입자 (The Particle in a Box, PIB)상자 속 입자 ( The Particle in a Box, PIB)어쩌다가, 입자는 상자에 빠지게 되었나... 0. 들어가기 수업을
stachemi.tistory.com
