데이비슨-거머 실험 (Davisson-Germer Experiment)
데이비슨-거머 실험 (Davisson-Germer Experiment)
너는 좋은 사람이야? 아니면 나쁜 사람이야?
1927년 미국 물리학자인 클린턴 데이비슨(Clinton J. Davisson, 1881-1958)과 레스터 거머(Lester H. Germer, 1896-1971)는 루이 드 브로이가 제안한 입자-파동 이중성을 확인하는 실험을 실시했다. 이들의 실험은 '파동(wave)'과 '입자(particle)' 개념이 자연에서 발견되는 어떤 대상을 보다 잘 설명하기 위해 도입된 이상적인 모델(모형) 일뿐이며, 자연의 실체는 '입자' 또는 '파동' 중 하나로 명확하게 구분될 수 없음을 보여주었다.
광자, 전자, 원자들까지도 파동성과 입자성을 동시에 갖고, 이러한 입자-파동 이중성이 자연의 본래 모습이라는 것을 알려주었으며, 어떤 대상이 갖는 파동성과 입자성 중에 어떤 특성이 나타날 것인지는 관찰 조건에 따라 달라질 뿐임을 보였다.
[참고] 당신은 좋은 사람인가? 아니면, 나쁜 사람인가? 둘 중 하나로 분명하게 정의될 수 있는가?
어떤 사람에 대해, 좋은 사람이라고 판단할 수 있는 행동이 평소 자주 관찰되어 그를 좋은 사람이라 생각했다 하더라도, 특정 상황이나 처한 환경에 따라 의외의 이기적이고 나쁜 면을 관찰했다면, 기존에 품었던 생각이 위협받거나 완전히 달라질 수 있다. 이 경우 그의 본성은 선한가? 아니면, 악한가? 그는 둘 중 하나로 분명하게 구분될 수 있는가?
드 브로이의 입자-파동 이중성은 어떤 사람(대상)이 좋은 사람(입자)인지, 나쁜 사람(파동)인지는 이미 결정되어진 고유 성질이라기보다, 처한 환경(관찰되는 조건)에 따라 좋은 사람처럼 보이는 행동(입자성)과 나쁜 사람처럼 보이는 행동(파동성)이 관찰되는 것일 뿐이며, 모든 사람은 좋은 면과 나쁜 면을 동시에 가짐을 말하는 것과 같다.

1. 전자 회절
두 개의 파동이 같은 지점을 지나갈 때, 서로 간섭이 일어난다. 파동의 봉우리와 봉우리, 또는 골짜기와 골짜기가 만나면 보강 간섭(constructive interference)이 일어나서 더 큰 진폭을 갖게 하며, 한 파동의 봉우리와 다른 파동의 골짜기가 만나면, 상쇄 간섭(destructive interference)이 일어나 진폭이 줄거나 0이 된다.

만약 어떤 파동이 이중 슬릿을 지나가게 되면, 틈새로부터 스크린을 향해 나아가는 파동들이 보강(wave match)과 상쇄(wave cancel)가 반복적으로 일어나서 회절 패턴이 관찰되게 된다. 아래 그림의 회절 패턴에서 밝은 부분이 보강 간섭, 어두운 부분이 상쇄 간섭에 의한 것이다.

따라서 드 브로이의 제안처럼 전자가 파동성을 갖는다면, 전자도 빛처럼 이중 슬릿 통과 이후 회절 무늬를 만들어낼 수 있을 것이며, 드 브로이의 가정을 검증될 수 있다.
당시, 엑스선(파동)이 단결정 고체에 의해 회절 현상을 일으킨다는 것이 알려져 있었는데, 이 회절 현상의 원인은 쬐어준 엑스선의 파장 길이와 고체 결정의 반복적이고 연속적인 입자 간격(거리)이 비슷했기 때문이었다. 만약, 전자가 파동성을 갖고, 고체 결정 간격이 전자의 파장 길이와 비슷하다면, 엑스선과 단결정 고체에 의한 회절과 유사한 현상을 관찰할 수 있을 것이다.


2. 데이비슨-거머의 실험
데이비슨과 거머는 진공 상태에서 낮은 에너지를 가진 전자의 흐름을 만들었다. 그리고, 이를 금속 니켈(Ni) 결정에 쬐어 주었다. 전자에 걸어주는 전압을 조절하여 운동 에너지를 20 ~ 200 eV 사이로 조절해 주었으며, 전자의 파장이 연속적으로 변화할 수 있도록 했다.
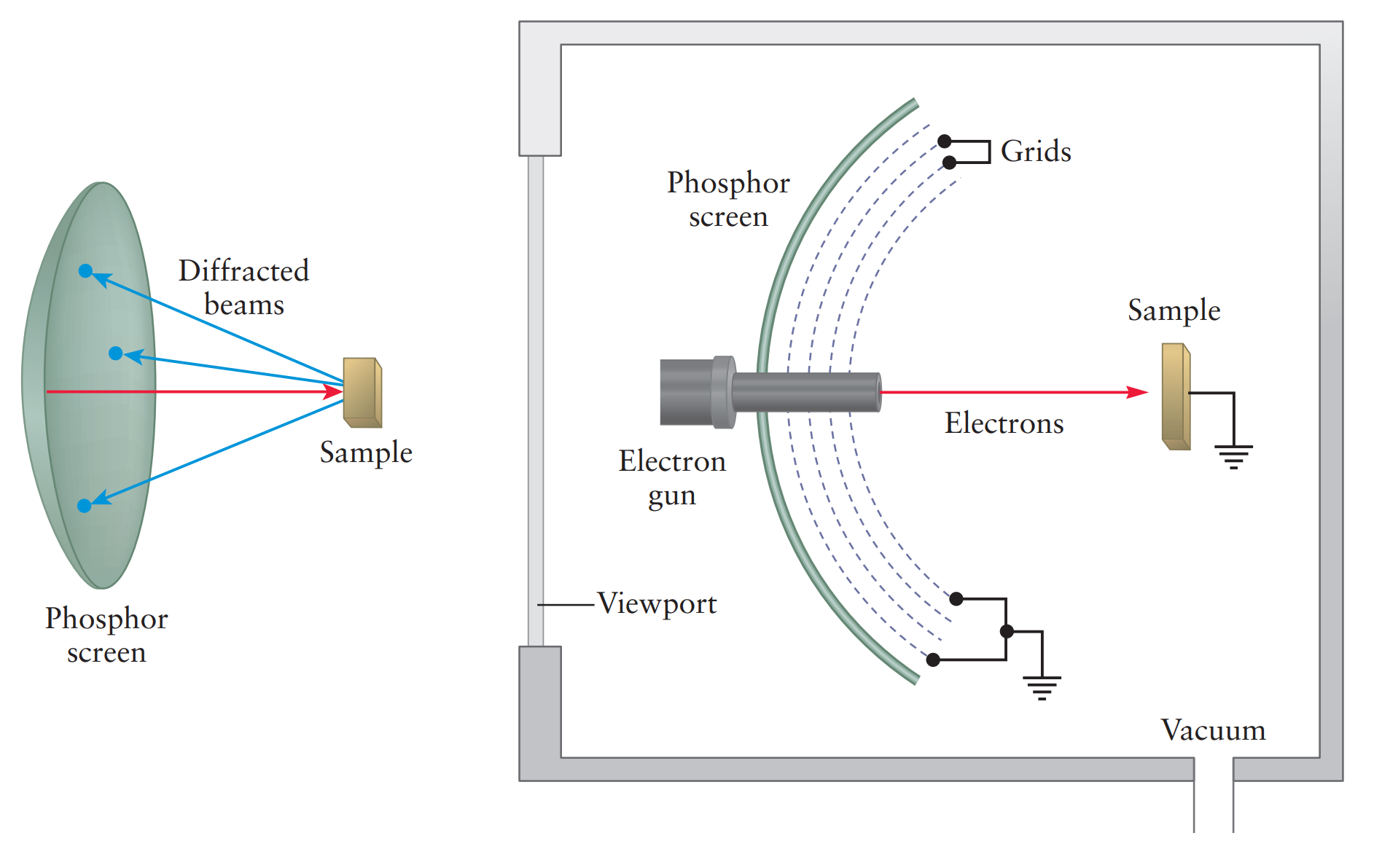
실험 장치를 간단히 설명하자면, 전자총(electron gun)으로부터 발사(→)된 전자의 흐름은 금속 니켈(sample) 표면에 충돌한 뒤 산란되어 인광 스크린(phosphor screen)에 닿게 되고, 회절 무늬를 만든다.
정지해 있던 전자를 V 라는 전압으로 가속시킨다면, 전자의 운동 에너지(E )는 전자의 전하량(e)에 가해진 전압(V)을 곱하여 나타낼 수 있다.

또한, 발사된 전자의 질량이 m 일 때, 전자의 운동량(p)과 운동 에너지(E ) 식을 바탕으로 다음과 같이 식을 정리할 수 있다.
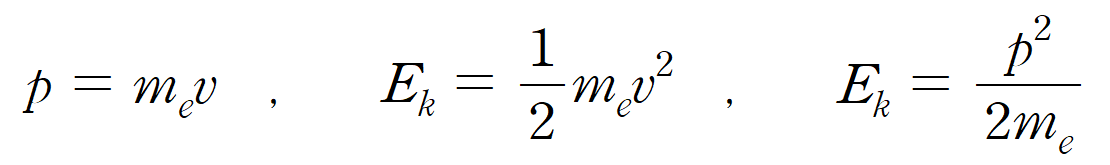
앞선 운동 에너지(E = eV ) 식을 대입하여, 운동량(p)에 관해 정리해주면 다음과 같이 표현된다.
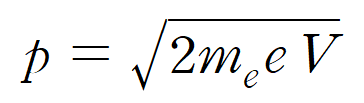
위 운동량 식에 드 브로이의 입자-파동 이중성에 관한 식(λ = h/p )을 대입하면, 전자의 파장(λ)은 다음이 표현된다.
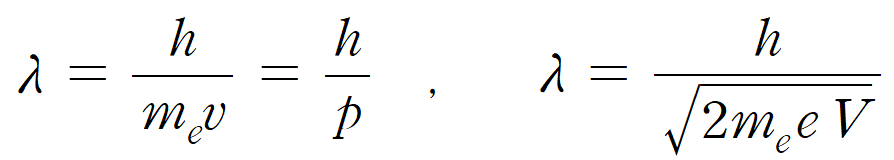
데이비슨과 거머의 전자 회절 실험에서 사용된 전형적인 운동에너지(E ) 값은 54 eV 였는데, 위 공식을 통해 계산된 전자의 파장(λ) 값은 약 0.167 nm 이다.
-
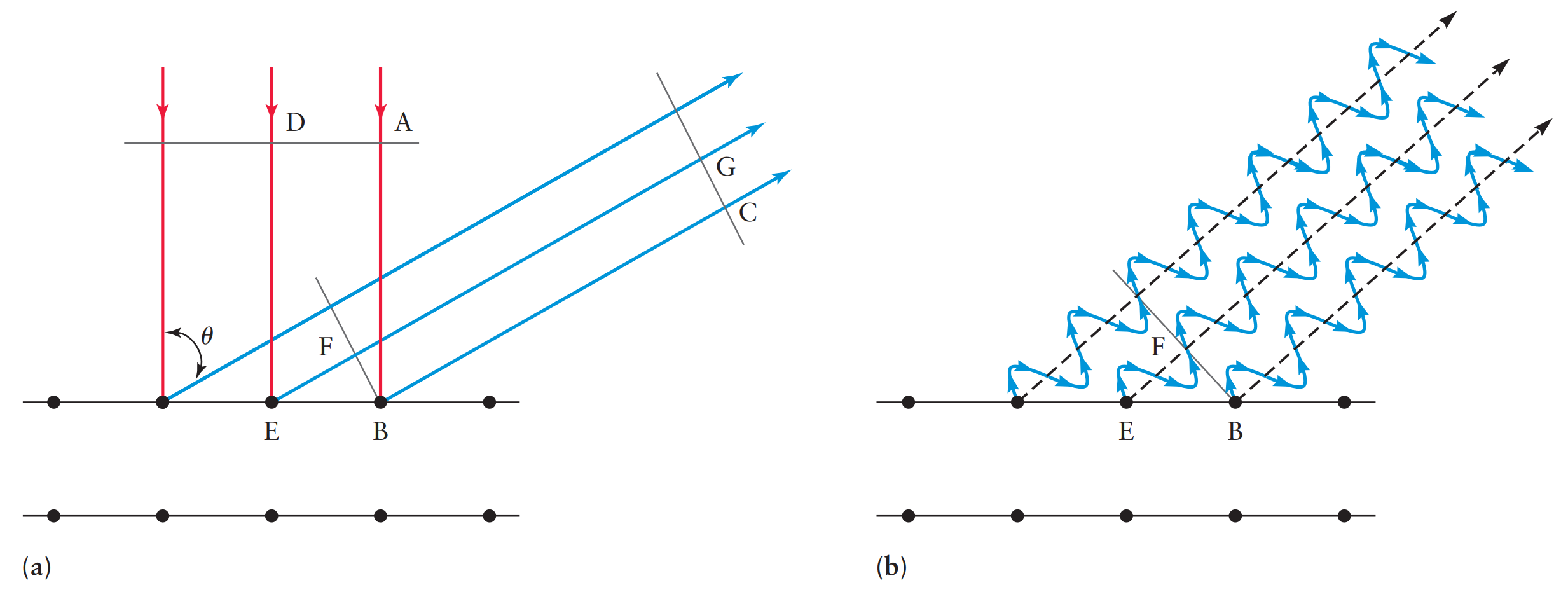
이 값은 엑스선 회절 실험을 통해 얻어낸 니켈 결정 원자 사이 간격(a) 0.182 nm 값과 회절 된 각도(θ ) 50˚ 를 대입하여 브래그 법칙(Bragg's Law, nλ = 2d sinθ )을 통해 계산한 파장 값인 0.165 nm 와 거의 같다.
3. 마치며,
데이비슨과 거머의 실험은 전자 회절을 보여줌으로써 드 브로이의 입자-파동 이중성에 관한 가설을 확인해 주었다. 또한, 이들의 실험은 발전하여 저에너지 전자 회절(LEED, Low-energy electron diffraction)이라는 현대적인 기술로 고체 표면 연구에 널리 활용되고 있다. 특정한 값의 운동에너지(E )로 발사된 전자의 회절각(θ )을 측정함으로써 결정 원자 사이 간격(a)을 측정한다.

[참고 및 출처]
* Oxtoby, Principles of Modern Chemistry 7th, 162-165p
* C. Davisson, L. H. Germer (1927). "Diffraction of Electrons by a Crystal of Nickel" , Physical Review. 30 (6): 705–740.
데이비슨-거머 실험
- 끝 -
* 끝까지 읽어주셔서 감사합니다.
