2024학년도 대학수학능력시험(2023.11.16.) 화학1 풀이 [1~20번]
2024학년도 대학수학능력시험(2023.11.16.) 화학1 풀이 [1~20번]
마감 기일 때문에 아주아주 빠듯했던 1년짜리 프로젝트가 금요일에 끝났다. 아직 심층면담이 남긴 했지만, 크게 걱정은 되지 않는다. 올해 11월 일정은 가히 살인적이었던 것 같다. 일주일 동안 평균 수면 시간이 3시간 남짓이었다.
어쩌다 보니 그 사이에 수능도 끝났다. 수능시험장 운영도 거쳐 간 업무 중 하나긴 했다. 수능이 끝난 당일에는 피곤했는지 의자에 앉아서 잠들어버렸다. 수능 문제도 주말이 되어서야 처음부터 제대로 보았다.
일단, 정리되기 전의 풀이라도 대충 블로그에 올려두어야 다른 일로 미루지 않을 것 같아서 부끄러운 날것의 풀이를 올린다.
정석대로가 아닌, 그냥 모니터에 문제를 띄워놓고 블로그에 직접 타이핑하면서 풀어서 중간중간 논리적 비약과 오류가 있을 수도 있다. 시간이 날 때, 최대한 수정해 보겠다.
어쨌든, 올해 화학1 한정으로 킬러는 없어 보인다. 마음에 들지 않는 문제들이 있긴 하지만, 성취기준상, 교육과정상, 수능을 통해 변별을 해야 한다는 부수적인 목적상 어쩔 수 없음을 이해한다. 내가 4면 끝까지 막힘없이, 올바른 답을 구해냈다는 것에 의미를 둔다.(칭찬)
사실, 풀어보고 싶은 것은 화학2 문제 이긴 하다.(우리 학교는 수능 화2 선택자가 화1 선택자보다 많았다.) 그러고 보니 작년 수능 문제 풀이도 마무리를 짓지 않은 것 같다. 모르겠다. 일단 시작해 보자.

정답 : ③ ㄱ, ㄷ
풀이 :
ㄱ. 에탄올은 탄소화합물이다. (참)
ㄴ. 에탄올이 증발하는 과정은 흡열 반응으로, 주위 열을 흡수한다. (거짓)
ㄷ. 철의 산화 반응은 발열 반응이므로, 주위에 열을 방출하고, 주위 온도가 높아진다. (참)

정답 : ⑤ ㄱ, ㄴ, ㄷ
풀이 :
X는 이온이 되면서 껍질수가 감소하여 반지름이 작아지고, Y는 이온이 되면서 유효핵전하 감소로 반지름이 증가한다. X는 양이온이 되려는 경향성이 있는 금속, Y는 음이온이 되려는 경향성이 있는 비금속이다.
ㄱ. 금속은 고체 상태에서 전성(펴짐성)이 있다. (참)
ㄴ. Y는 안정한 이온이 되면서 반지름이 증가하므로, Y 이온은 음이온이다. (참)
ㄷ. 안정한 X 양이온과 Y 음이온 사이에 X2Y 가 형성된다는 것은 양이온과 음이온의 전하비가 1 : 2라는 뜻이다. (참)

정답 : ④ 9
풀이 :
균형 잡힌 화학반응식을 나타내면 다음과 같다.
6HF(g) + 2Al(s) → 2AlF3 (s) + 3H2 (g)
고체 Al 2 몰이 반응하면, H2 3 몰이 생성된다. 예를 들어 Al 54 g(=2 몰)이 반응하면, 기체 H2 6 g(=3 몰)이 생성된다는 뜻이다. 따라서 x/y =54/6 = 9 이다.

정답 : ④ ㄱ, ㄴ
풀이 :
매번 밀폐된 용기에서의 물의 증발과 수증기 응축 사이의 평형 문제로 출제되다가, 올해 9월 모의고사에서 처음 이산화탄소 승화 개념을 문제에 적용 시도하고, 별 문제가 없었기에 수능에서도 승화 개념이 나온 것이 아닌가 싶다. 뭐, 물의 증발 응축 사이 평형과 다르지 않다. 출제자 입장에서는 승화는 방향을 언급해줘야 하니, 문제 표현만 더 귀찮아지지 않았을까 싶다.
문제로 돌아와서, 결론에서 학생의 가설이 옳다고 했고, 결론 또한 타당했다고 제시되었으므로 가설에서는 드라이아이스와 기체 이산화탄소 평형 상태에서의 올바른 특징이 나타나야 한다. 탐구 과정에서 드라이아이스의 질량 변화를 측정했으므로, 질량에 관한 가설이 나와야 탐구 전반적으로 완벽하다. (그런데, 실험적으로 드라이아이스와 기체 이산화탄소가 함께 있는 계에서 드라이아이스만의 질량은 어떻게 측정했을까? 실험적으로 궁금하다.)
ㄱ. 드라이아이스의 질량이 평형 상태에서 변하지 않는다는 보기는 적절하다. 탐구 결과를 통해서도 평형에 도달한 t2 시간 이후에 드라이아이스 질량이 변하지 않는 것(일정)을 확인할 수 있다. (참)
ㄴ. 평형에서는 정반응의 속도와 역반응의 속도가 같다. t1일 때는 평형 도달 전이며, 고체 → 기체 속도(분모항)가 기체 → 고체 속도(분자항) 보다 우세하다. 따라서 보기의 값은 1보다 작다. (참)
ㄷ. t3는 평형 이후로, 고체→기체, 기체→고체 상변화는 계속해서 일어난다. 언제나 그렇듯 동적평형 개념을 알고 있는지 확인하는 보기다. (이것이 주요 성취기준이기에 푸는 사람 입장에서는 뻔하지만, 출제자 입장에서는 보기 하나는 관련된 내용으로 출제할 수 밖에 없다.) (거짓)
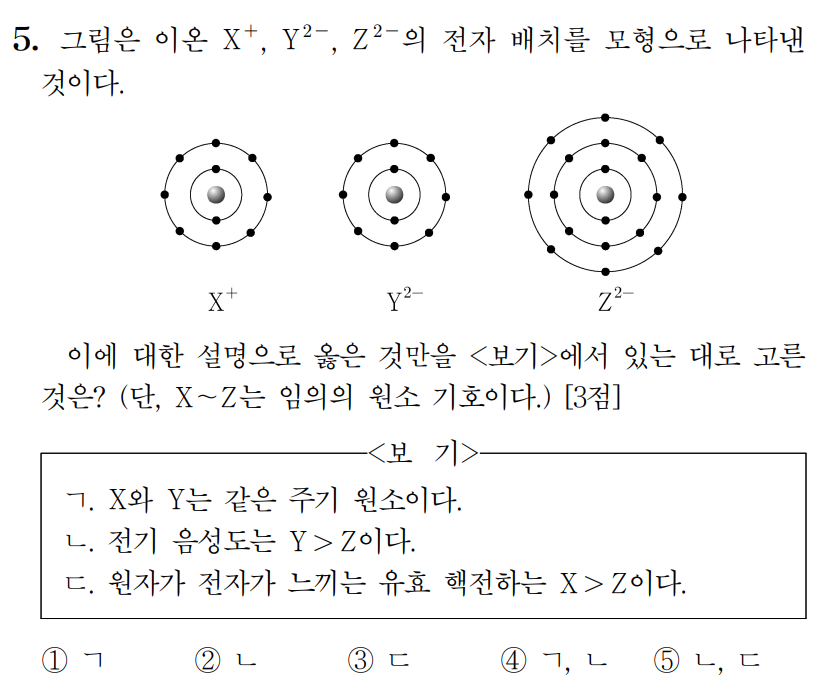
정답 : ② ㄴ
풀이 :
이온의 전하와 전자배치 모형을 통해, X는 3주기 1족 나트륨(Na), Y는 2주기 16족 산소(O), Z는 3주기 16족 황(S) 이다.
ㄱ. 나트륨(X)과 산소(Y)는 서로 다른 주기 원소이다. (거짓)
ㄴ. 전기음성도는 산소(Y)가 황(Z)보다 크다. 전기음성도는 같은 족에서 껍질수가 작을수록(↑) 증가한다. (참)
ㄷ. 같은 주기에서 원자가 전자가 느끼는 유효핵전하 크기는 원자번호가 증가할수록(→) 증가한다. 따라서 나트륨(X)보다 황(Z)의 유효핵전하가 크다. (거짓)

정답 : ② ㄷ
풀이 :
X, Y, Z는 2주기 원소이고, 분자 1 몰의 존재 원자수 비를 통해 분자를 찾아내야 한다. 사실 직관적으로 푸는 것이 이유를 찾아가며 푸는 것보다 빠르다. 일단, 후보를 좁혀보자.
(가)의 후보는 HF, N2H2, C2H2, H2O2 등등... , (다)의 후보는 HCN, HNO, HOF 정도이다. 결국 이를 좁혀주는 것은 Y에 의해서이고, (나)의 H : Y = 1 : 2라는 결합 비에 의해서 (가)와 (다)에 해당하는 물질이 좁혀질 것이다.
수소와 2주기 원소가 옥텟규칙을 만족하면서 1 : 2의 비율로 결합한다는 것은 (나) = H2O 밖에 없다. Y = 산소(O)이므로, (가)는 HF이고, X = 플루오린(F) 이다. 자연스레 (다)는 HOF가 된다.
ㄱ. (가) = HF에는 2중 결합이 없다. (거짓)
ㄴ. (나) = H2O는 극성 공유 결합만 존재한다. (거짓)
ㄷ. HOF에서 F는 부분적인 음전하를 띤다. (참)

정답 : ③ ㄱ, ㄴ
풀이 :
(가)는 CO2, (나)는 COF2, (다)는 O2F2이다.
ㄱ. 다중결합이 있는 물질은 CO2, COF2이다. (참)
ㄴ. (가) CO2는 극성공유결합을 갖지만, 직선(대칭) 구조로 무극성 분자이다. (참)
ㄷ. 공유 전자쌍의 수는 (가) = 4쌍, (나) = 4쌍, (다) = 3쌍이다. (거짓)

정답 : ① ㄱ
풀이 :
언제나 이런 수수께끼형 문제는 어렵다기보다는 풀기 귀찮다. 2주기, 3주기, 15 ~17족 원소이면, N, O, F, P, S, Cl 이다.
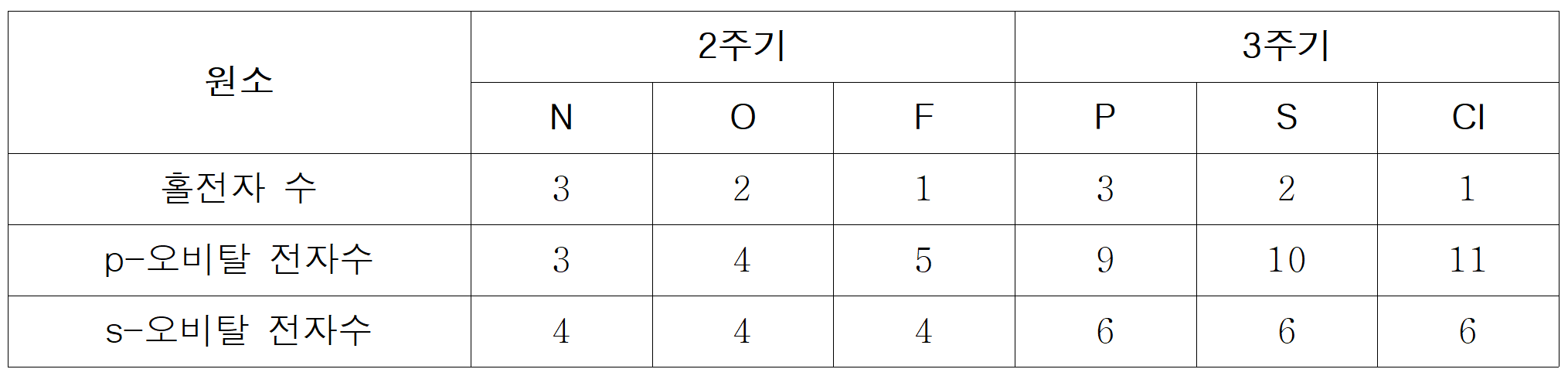
문제의 조건을 하나씩 살펴보면, W와 Y는 서로 다른 주기이면서, [p-전자수/홀전자수]가 같다고 했다. 여기에 부합하는 원소는 F(=5/1)와 S(=10/2) 뿐이다.
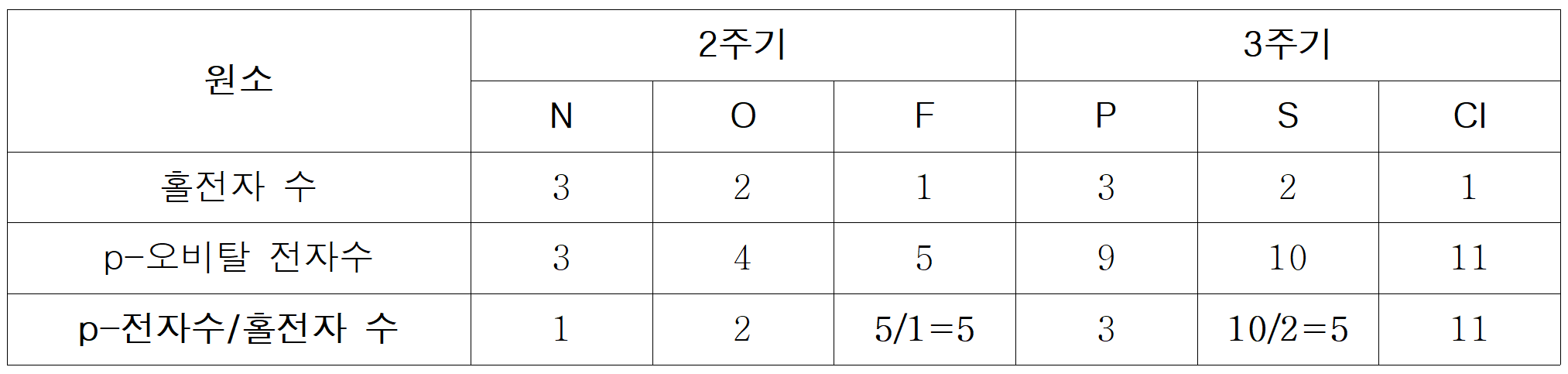
F와 S의 [홀전자수/s-전자수]는 각각 F=1/4, S=1/3 이다.
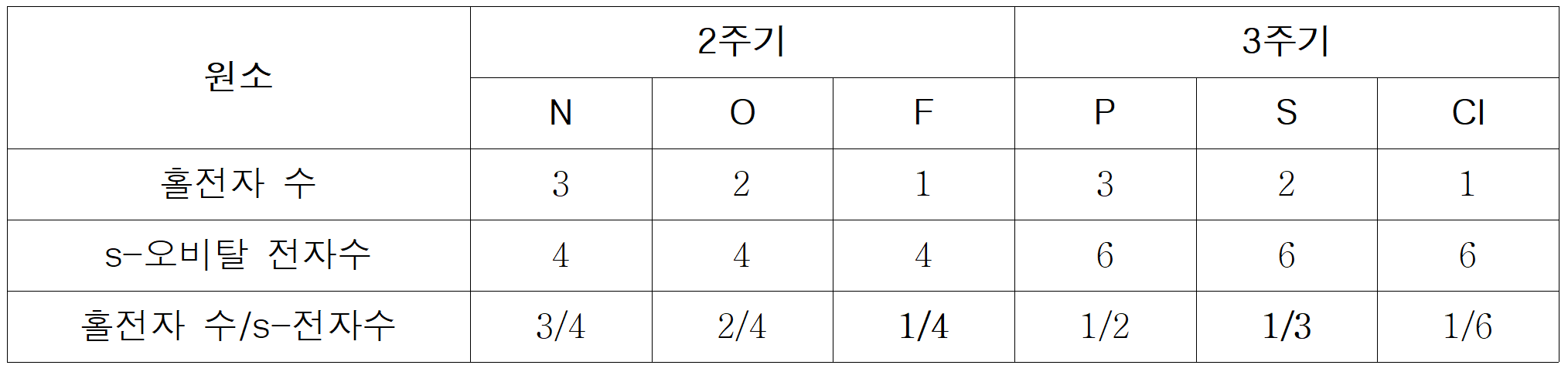
만약, Y = F라면, Z는 Y의 절반 값인 =1/8 또는 =2/16 등이 존재해야 한다. 그런데, 해당하는 원소가 없다. 반면, Y = S라면, Z는 Y의 절반 값인 =1/6 이 되어야 하며, 이에 부합하는 Z는 Cl(=1/6)이다.
자연스럽게 W = F 이다. Y = S 이므로, X는 Y의 9/4배가 되어야 하고, =(9/4)*(1/3) =3/4가 되어야 한다. 따라서 X = N(=3/4) 이다. 정리하면, W = 플루오린(F), X = 질소(N), Y = 황(S), Z = 염소(Cl) 이다.
ㄱ. 3주기 원소는 Y(=S), Z(=Cl), 2가지이다. (참)
ㄴ. 원자가 전자 수는 W(=F, 7개)와 Z(=Cl, 7개)가 같다. (거짓)
ㄷ. 전자가 들어있는 오비탈 수는 X(=F) 5개, Y(=S) 9개로 Y > X 이다. (거짓)

정답 : ⑤ ㄱ, ㄴ, ㄷ
풀이 :
실험과정 (나)에서 넣어준 B가 모두 B2+가 되었고, A+ 이온 일부가 석출 되었다. 실험과정 (다)에서 넣어준 C는 (나)에서 남아있던 A+ 이온과 반응하여 Cm+ 이온이 되었다. 초기 (가)의 전하량은 +15N 이다. 반응을 완료한 이후에도 +15N 은 만족해야 한다.
15A+ → (15-x) A+ + (x/2) B2+ 이다.
전체 이온수가 12N 이므로, (15-x + (x/2)) = 12이다. 30 - 2x + x = 24 이므로, x = 6이다. 즉,
6N A++ → 3N B2+ 로 대체되었다.
(나)에서 남아있는 A+는 9N 이며, (다)에서 모두 반응하여 3N 의 Cm+를 생성한다.
ㄱ. 9A+ → 3Cm+ 관계를 만족하므로, C 이온의 전하량 m = +3이다. (참)
ㄴ. (나)와 (다)에서 A+은 금속 B와 C로부터 전자를 받아 석출(환원)되므로, 산화제로 작용한다. (참)
ㄷ. (다) 과정 이후 용액에는 B2+ 3N , C3+ 3N 이 존재하므로, 1 : 1이다. (참)

정답 : ③ ㄱ, ㄷ
풀이 :
바닥상태 탄소 원자이며, 가능한 오비탈은 1s, 2s, 2p?, 2p? 이다. 제시된 조건에서 n - l 의 가능한 수는 2-0=2, 2-1=1, 1-0=1 세 가지이다. (나)보다 (가)가 n - l 값이 크기 위해서는 (가) = 2s 이어야만 한다.
l - ml 조건은 0-0=0, 0-0=0, 1-(-1)=2, 1-(0)=1, 1-(+1)=0 이므로, 가능한 경우는 0, 0, 2, 1, 0이다. (다)는 2p-1 또는 2p0 이어야만 하며, (나)와 (라)는 1s, 2p+1 중 하나이다.
(나)와 (라)를 구분해 보기 위해 마지막 조건을 사용하면, (n+l+ml) / n 값은 1s = (1+0+0)/1 = 1 이며, 2p+1 = (2+1+1)/2 = 2이다. (라) > (나) 이므로, (라) = 2p+1, (나) = 1s 이다.
<보기>를 해결하는 데는 필요 없지만, (다)의 정체를 찾아보면, (나) 1s와 같은 (n+l+ml) / n 값을 갖기 위해서는 (2+1+ml)/2 = 1이므로, ml = -1임을 알 수 있다. (다) = 2p-1이다.
ㄱ. (나)는 1s이다. (참)
ㄴ. (다)는 2p-1이든, 2p0이든 상관없이 바닥상태 탄소 원자이므로 1개의 전자가 채워진다. (거짓)
ㄷ. 다전자 원자의 에너지 준위는 n + l 값에 의존하며, (라) = 2p+1 > (가) = 2s 이다. (참)
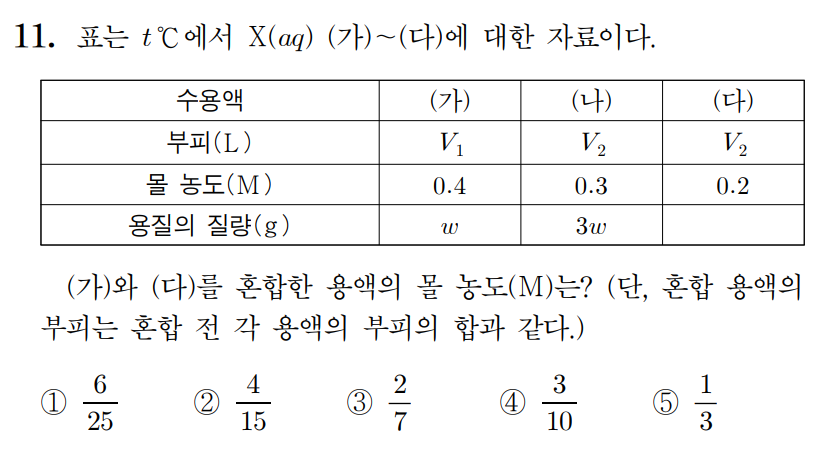
정답 : ① 6/25
풀이 :
용질의 질량으로 주어졌지만, 용질의 종류가 X로 같으므로, 화학식량을 w [g/mol]이라 생각하면, (가) = 1 mol, (나) = 3 mol의 용질이 포함되었다고 생각할 수 있다.
(가)의 농도가 0.4 M, (나)의 농도가 0.3 M이므로,
(가)의 부피 V1 = 1 [mol] / 0.4 [mol/L] = 2.5 L , ...
(나)의 부피 V2 = 3 [mol] / 0.3 [mol/L] = 10 L 이다.
(다)의 부피는 (나)와 같은 V2 = 10 L 이고, 몰농도가 0.2 M이므로, 포함된 몰수는 2 mol이다.
(가)와 (다)를 혼합하면, 전체 용질 = 1+2 = 3 mol, 전체 부피는 2.5+10 = 12.5 L 이므로 몰농도는,
3 mol / 12.5 L = 6/25 M 이다.

정답 : ② 5/6
풀이 :
산화수, 반응한 전자수, 반응 전후 전하균형 등을 모두 활용하는 문제이다. 산화-환원의 경우 앞의 세 가지만 따져주면, 어지간한 문제는 해결할 수 있다. 문제에 주어진 원소 기호가 X와 Y로 가려져있어도 실제 기호가 보이는 것 같지만... 모르는 척 풀어보자. (사용될 수 있는 복잡한 예시가 몇 가지 없다.)
반응 (가)에서 Br의 산화수 변화는 +5에서 -1로 변하며, 산화수가 6만큼 감소한다. 이는 X 3개의 총 산화수 변화가 +6이라는 뜻이다. X 하나당 산화수는 2만큼 증가해야 한다. XO33-에서의 X산화수는 +3, XO43-의 X산화수는 +5이다.
반응 (가)의 생성물 X 산화수/반응물 X 산화수 = 5/3
반응 (나)에서 반응물 X 산화수는 +3이며, 제시된 조건(= (가), (나) 생성물 X 산화수/반응물 X 산화수 = 5/3)에 의해 반응 후 X 산화수는 +5이다. 따라서 m = 5이다.
또한, 제시된 조건에서 반응 (가)에서 산화수가 가장 큰 값 a의 값이 같다고 했으므로, a = 5이며, 반응 (나)에서 관여한 전자의 총 수는 20이다. 반응식을 완성하면,
5 X2O3 + 4 YO4- + b H+ → 5 X2O5 + 4 Yn+ + c H2O
반응 (나)의 YO4-에서 Y의 산화수 = +7이고, 총 4개의 Y가 반응해야 하며, 관여한 전자수는 20이므로, Y 한 개당 산화수 변화는 -5이며, 반응 후 Y의 산화수 = +2가 되어야 한다. 따라서 n = 2 이다.
반응 전후의 전하가 +8로 균형이 유지되어야 하므로, -4 + b = +8 이 되어야 한다. b = 12 이다.
문제에서 요구하는 m*n / b = 5*2 / 12 = 5/6 이다.
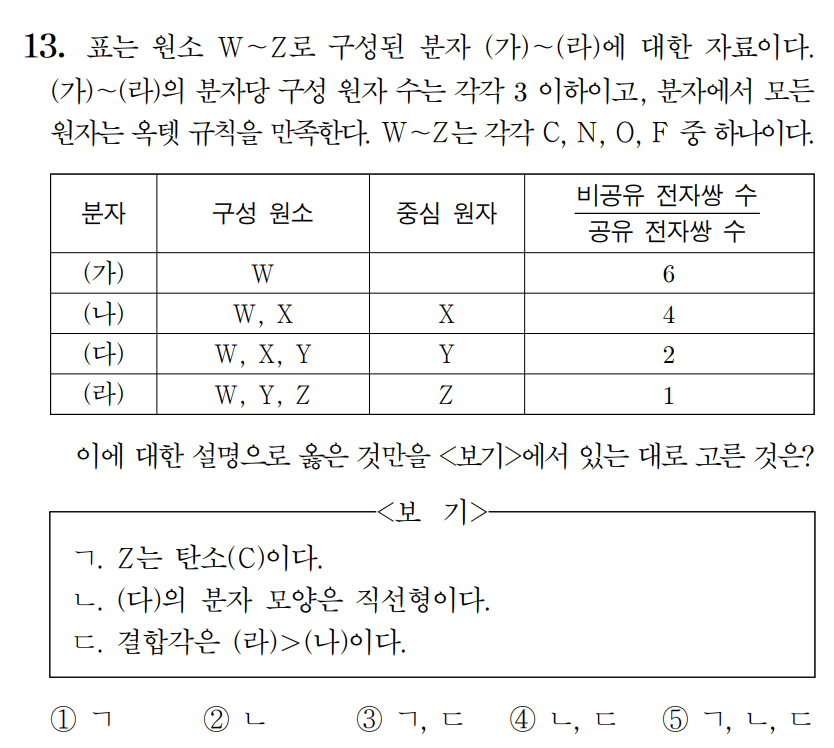
정답 : ③ ㄱ, ㄷ
풀이 :
(가)는 홑원소 물질이다. N2, O2, F2 중에 비공유e/공유e = 6을 만족하는 것은 F2 뿐이다. W = 플루오린(F)이다.
(나)부터 (라)까지는 플루오르화물을 찾는 문제가 되겠다. 분자당 구성 원자수가 3 이하이므로, (다)와 (라)는 ONF, FCN 중 하나이다. (다)와 (라)에서 Y를 공통으로 가지고 있으니 Y = 질소(N)이다. 중심원자가 Y인 (다) = ONF, 중심원자가 Z인 (라) = FCN이다. 따라서 X = 산소(O), Z = 탄소(C) 이다. (나)는 OF2이다.
(나)~(라)의 화합물과 표의 비공유e/공유e 값을 검토해 보자.
(나) = OF2 (비공유e/공유e = 8/2 = 4)
(다) = ONF (비공유e/공유e = 6/3 = 2)
(라) = FCN (비공유e/공유e = 4/4 =1)
ㄱ. Z는 탄소이다. (참)
ㄴ. (다) ONF의 분자 모형은 굽은형이다. ONF 는 AX2E1 타입이다. (거짓)
ㄷ. 결합각은 직선형의 FCN이 굽은형의 OF2 보다 크다. (참)

정답 : ⑤ ㄱ, ㄴ, ㄷ
풀이 :
원자 A ~ D는 원소 X와 원소 Y의 알맹이들이다.
원자 A는 중성자수(n) - 양성자수(p) = 0 이며, 중성자수(n) + 양성자수(p) = m-1 이다. 두 식을 빼하면, 2양성자수(p) = m-1이다. 같은 방식으로, 원자 B, C, D를 하면,
원자 B는 n - p = 1 , n + p = m-2 이다. 2p = m-3
원자 C는 n - p = 2 , n + p = m+1 이다. 2p = m-1
원자 D는 n - p = 3 , n + p = m 이다. 2p = m-3
따라서 A와 C가 같은 원소(p=(m-1)/2)이며, B와 D가 같은 원소(p=(m-3)/2)이다. 원자 번호가 X > Y 이므로, A와 C는 X 원소, B와 D는 Y 원소이다. X(=(m-1)/2)와 Y(=(m-3)/2)의 원자번호 차이는 1 차이이다. (ㄱ 보기, 참)
A ~ D의 중성자 수를 계산해 보면,
A의 중성자 수는 양성자 수와 같으며, 0.5m-0.5 이다. C의 질량수가 2만큼 크므로, C의 중성자 수는 A보다 2가 크며, 0.5m+1.5 이다. B의 중성자 수는 양성자 수보다 1개 많으며, 0.5m-1.5+1 = 0.5m-0.5 이다. D의 질량수가 B보다 2만큼 크므로, 중성자 수는 B보다 2 많으며, 0.5m+1.5 이다.
A ~ D의 중성자 합이 76이므로, 0.5m-0.5 + 0.5m+1.5 + 0.5m-0.5 + 0.5m+1.5 = 76 이다. 2m +2 = 76 이다. m = 37 이다.
A의 질량수 = 36, D의 질량수 38, 원소 X의 원자번호 18이다.
B의 질량수 = 35, D의 질량수 37, 원소 Y의 원자번호 17이다.
ㄴ. 같은 질량(g)에 들어있는 A와 C의 중성자 수(mol)를 비교하자.
36 g의 A = 1 mol의 A 이며, 1 mol의 A = 18 mol(중성자)이다. 즉, 36 g = 18 mol(중성자) 이다. 반면, C는 38 g의 C = 1 mol의 C이며, 1 mol의 C = 20 mol(중성자)이다. 즉, 38 g = 20 mol(중성자) 이다.
A는 1g = 18/36 = 1/2 mol(중성자) 이며, C는 1g = 20/38 = 10/19(중성자) mol 이다. 따라서 C(중성자)/A(중성자) = 20/19 이다. (참)
ㄷ. 1 mol의 D에 들어있는 양성자수는 17 mol이며, 1 mol의 A에 들어있는 양성자수는 18 mol이다. 따라서 D(양성자)/A(양성자) = 17/18 < 1 이다. (참)
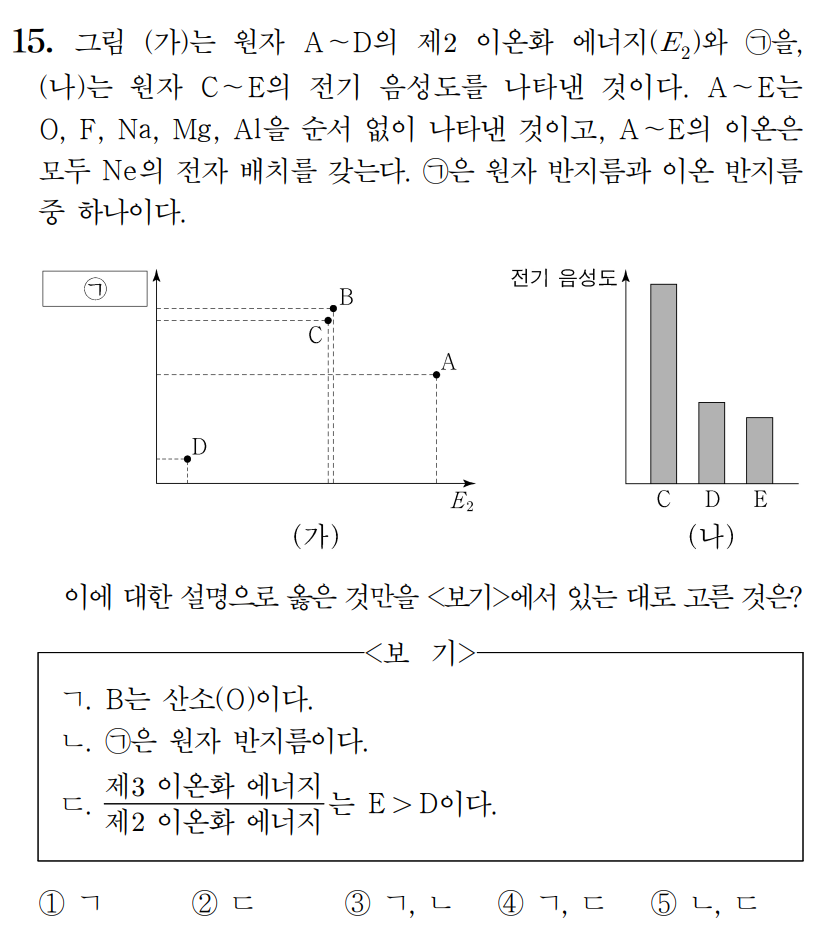
정답 : ④ ㄱ, ㄷ
풀이 :
A, B, C, D, E는 O, F, Na, Mg, Al 이며, 전기음성도는 비금속인 O, F 가 금속인 Na, Mg, Al 에 비해 매우 크다. 따라서 (나) 그래프에서 전기음성도가 큰 C는 O 또는 F 중 하나이며, D, E는 Na, Mg, Al 중 하나이다.
(가) 그래프를 살펴보면, 제2 이온화에너지(E2)가 가장 높은 값을 갖는 원소가 A이며, 원자가 전자가 1개인 Na 임을 할 수 있다. 따라서 D와 E는 Mg, Al 중 하나이다. 그러나 전기음성도가 D > E 이므로, D = Al, E = Mg 이다.
A = 나트륨(Na), D = 알루미늄(Al), E = 마그네슘(Mg)
이제 그래프 (가)의 B와 C를 비교해보면, 제2 이온화에너지(E2)가 약간 B > C 인데, F의 제2 이온화는 O의 제1 이온화처럼, O의 제2 이온화는 N의 제1 이온화처럼 취급할 수 있다. 제1 이온화 에너지는 N > O 이므로, 제2 이온화에너지 값이 큰 B = 산소(O), 작은 C = 플루오린(F) 가 된다.
B = 산소(O), C = 플루오린(F)
ㄱ. B는 산소이다. (참)
ㄴ. 만약 (가)의 y축 값이 원자 반지름이라면, 3주기 원소인 A와 D의 반지름이 2주기 원소인 B와 C보다 크게 나타나야 한다. y축이 이온 반지름임을 알 수 있다. (거짓)
ㄷ. 안정한 이온상태에서 세 번째 전자를 떼어내야 하는 Mg의 제3 이온화에너지는 너무나도 크다. Mg > Al 이다. (참)

정답 : ① dA / 20dB
풀이 :
산염기 중화 적정에서는 반응한 산의 몰수 = 반응한 염기의 몰수 식만 세우면 된다. 밀도를 주던, 질량을 주던 풀이는 같다. 식초를 묽히는 과정만 헷갈리지 않으면 될 듯하다. 초반에 5배로 묽히고, 절반만 사용했다.
그냥 초기에 식초 10 mL에 물 40 mL 넣어서 50 mL 만든 것과 과정상 똑같다.
(식초 A의 적정)
사용된 염기 = a M * 10 mL =10a mmol
초기 식초 A의 부피 = 20 mL → 밀도를 이용하여 질량으로 바꾸면, 20dA [g]의 식초
물을 첨가하여 100mL 만들고, 그중 50 mL만 취했으므로, 실제로는 초기 10dA [g]의 식초만 사용한 것과 같다.
10dA [g] 속에 포함된 아세트산의 질량은 1 g 에 0.02 g의 아세트산이 포함되어 있다는 것은 초기 농도가 2%라는 뜻이다. 10dA [g] 중에 2%만 아세트산이다. 즉, 10dA * 0.02 = 0.2dA [g]의 아세트산이 포함된 것이다.
그리고, B의 퍼센트 농도가 x% 이다.
(식초 B의 적정)
사용된 염기 = a M * 25 mL = 25a mmol
초기 식초 B의 부피 = 20 mL → 밀도를 이용하여 질량으로 바꾸면, 20dB [g] 식초
물을 첨가하여 100 mL 만들고, 그중 50 mL만 취했으므로, 역시 초기 10dB의 식초만 사용한 것과 같다.
식초 A의 적정 결과와 사용된 염기가 25 mL 라는 것에 따라 10dB의 식초에는 식초 A보다 2.5배의 아세트산이 더 들어있다. 따라서 식초 A에 포함된 아세트산의 2.5배의 아세트산이 식초 B에 존재한다.
즉, 10dB 속 아세트산의 양 = 0.2dA [g] * 2.5 = 0.5dA [g] 이 포함되어 있다. 이를 분율로 나타내면, 전체 10dB 중에 0.5dA의 아세트산이 포함되어 있으므로,
0.5dA / 10dB로 나타낼 수 있고, x = dA / 20dB 이다.

정답 : ⑤ ㄴ, ㄷ
풀이 :
pH와 pOH의 합은 14이다. (가)의 비율을 유지한 채 숫자를 바꾸어주면, pH = 1.5, pOH = 12.5 이다. (가)는 산성 용액이고, pH - pOH = 11이다.
(나)는 (가)보다 pH - pOH 값이 4가 작다고 했다. 즉, |pH - pOH | = 7 이다. 중성 용액은 pH와 pOH가 같아야 하므로, 해당 조건을 만족할 수 없다. (나)는 염기성이며, pH가 pOH보다 7 큰 값이다.
pOH + pOH + 7 = 14 , 2pOH = 7 , pOH = 3.5 이다. pH는 10.5 이다. x = 105/35 = 3 이다.
자연스럽게 (다)는 중성이며, pH = pOH 모두 7이다. y = 7/7 = 1 이다.
ㄱ. (나)의 액성은 염기성이다. (거짓)
ㄴ. x = 3 , y = 1 이므로, x + y = 4이다. (참)
ㄷ. (가)의 pOH = 12.5 이므로 OH- 몰농도는 10-12.5 M 이며, 몰수 a = 10-12.5 * 0.2 = 2 x 10-13.5 이며, 같은 방식으로 (나)와 (다)의 b, c를 모두 구하면, b = 10-3.5 * 0.4 = 4 x 10-4.5 , c = 10-7 * 0.5 = 5 x 10-8 이므로,
b x c / a = ( 4*5/2) x 10(-4.5-8+13.5) = (10) x 10 = 100 (참)
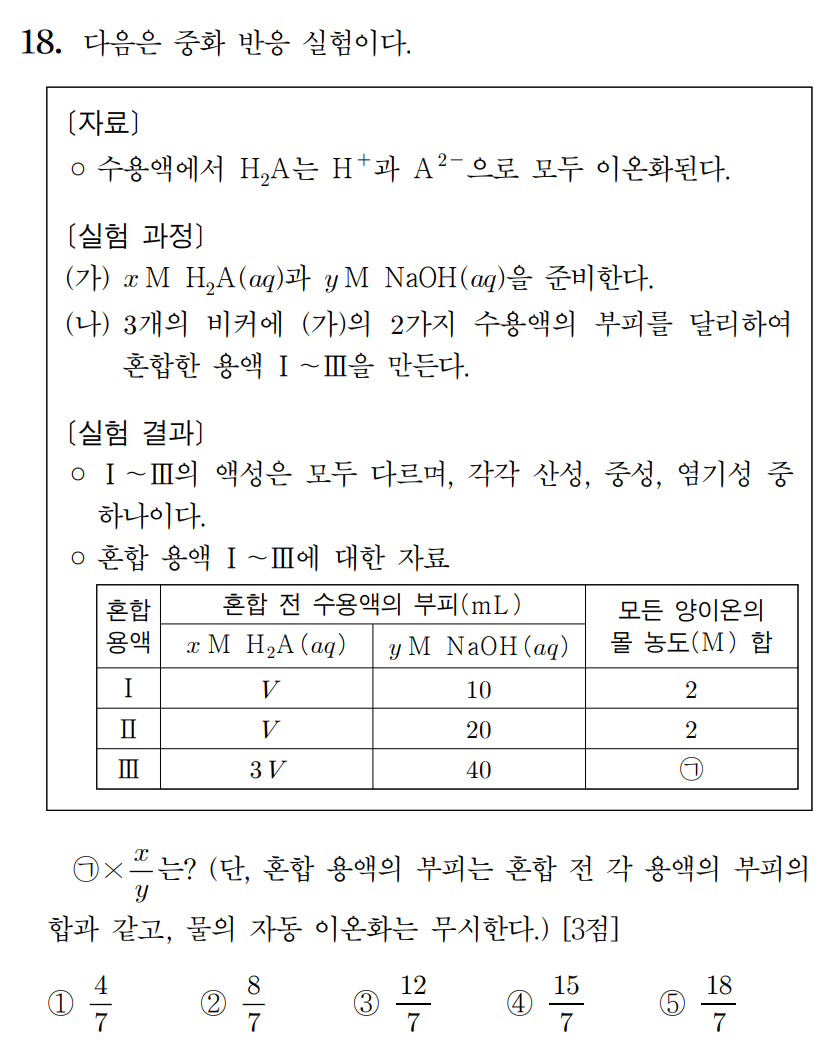
정답 : ② 8/7
풀이 :
모든 산의 부피를 3V라고 스케일을 키워서 생각하자. 실험 I은 3V + 30 mL , 실험 II는 3V + 60 mL , 실험 III는 3V + 40 mL 라고 생각하면, 혼합용액 I은 산성, II는 염기성, III는 중성이다.
6xV H+ = 40y OH- 이므로, 용액 I은 10y mmol 만큼 H+ 남아있으며, 용액 II는 20y mmol 만큼 NaOH가 더 첨가되었다. 용액 I과 II의 전체 양이온 몰농도가 같다고 했으므로,
40y / (3V+30) = 60y / (3V +60) 이며, 2/(3V+30) = 3/(3V+60) , 6V + 120 = 9V + 90 , 3V = 30 , V = 10 mL 이다.
따라서 용액 I의 양이온 농도가 2 M 이므로, 40y mmol / 60 mL = 2 이며, y = 3 이며, 6xV = 40y의 관계식에 따라 x = 2이다.
용액 III의 몰농도는 전체 부피 70 mL에 40y = 120 mmol이 포함되어 있으므로, 농도는 12/7 M 이다.
문제에서 요구하는 (ㄱ)*(x/y) = 12/7 * (2/3) = 8/7 이다.

정답 : ③ ㄱ, ㄷ
풀이 :
편의상 XaYb를 AB분자, XaXc를 AC 분자라고 하자.
AC 분자 수는 (가) : (나) = 2 : 1 이다. AB 분자수는 (가) : (나) = 2 : 3이다. 전체 기체의 부피가 4V로 같으므로, 비율 그대 2+2 : 3+1 로 몰수가 있다고 가정해도 무리가 없다.
(가)는 AB 분자 2몰 + AC 분자 2몰, (나)는 AB 분자 3몰 + AC 분자 1몰이라고 생각하자. 여기서 Y 원자수가 6 : 5 이므로, 각각의 분자에 대해 구해보면,
(가)의 AB 분자 내 Y원자 = 2몰*b = 2b 몰, AC 분자 내 Y원자 = 2몰*c = 2c 몰, 따라서 (가)의 총 Y원자 수 = 2b + 2c 이며,
(나)의 AB 분자 내 Y원자 = 3몰*b = 3b 몰, AC 분자 내 Y원자 = 1몰*c = 1c 몰, 따라서 (나)의 총 Y원자 수 = 3b + c 이며,
정리하면, 2b + 2c : 3b + c = 6 : 5 이다. 18b + 6c = 10b + 10c 이며, 8b = 4c 이고, b=1, c =2 라고 할 수 있다.
전체 원자수가 10N, 9N이라는 정보를 바탕으로,
(가)의 AB 분자 내 X원자 = 2몰*a = 2a 몰, AC 분자 내 X 원자 = 2몰*a = 2a, 따라서 (가)의 총 X 원자 수 = 4a 이며, X와 Y의 전체 원자수는 4a + 2b + 2c = 10N , b, c에 각각 1, 2를 대입했을 때, a = 1 이다.
(나)의 AB 분자 내 X원자 = 3몰*a = 3a 몰, AC 분자 내 X 원자 = 1몰*a = a, 따라서 (나)의 총 X 원자수 = 4a 이며, X와 Y의 전체 원자수는 4a + 3b +c = 9N b = 1, c = 2, a = 1 모두 만족한다.
ㄱ. a = b 이다. (참)
ㄴ. X의 원자량과 Y의 원자량을 구해보면, 2몰의 XY 의 질량이 15w 이고, 2몰의 XY2의 질량이 16w 이므로, 2몰의 Y 질량이 1w 이다. Y의 원자량은 0.5w이다. 즉, 2몰의 X 질량은 14w가 되며, X의 원자량은 7w 이다. X의 원자량/Y의 원자량 = 7/0.5 = 15 이다. (거짓)
ㄷ. 분자의 몰수는 5 몰이면서, Y의 원자수가 상대값 9를 갖는 경우는 XY 1몰, XY2 4몰인 경우다. 전체 입자수는 14가 되며, x = 14이다. (참)
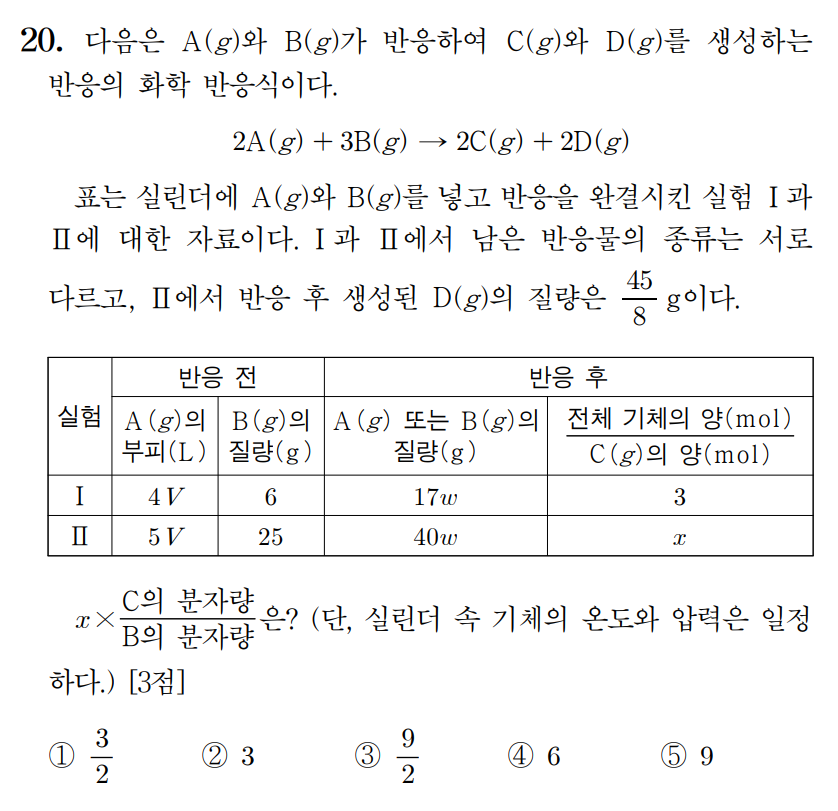
정답 : ④ 6
풀이 :
실험 I의 B는 6 g, 실험 II의 B는 25 g 이다. 만약, 실험Ⅰ에서 A가 한계 반응물이라면, A 4V 반응하는 동안 6 g을 모두 사용하지 못한다는 뜻이 된다. 화학 반응식 계수로 살펴보았을 때, A 4V가 4몰이라고 가정한다면 B 6 g은 6몰이 안된다는 뜻이며, 만약, 5V를 반응시키면, 여전히 25 g의 B는 여전히 남게 된다.
이에 실험 I은 B가, 실험 II는 A가 한계 반응물이다. 실험 I의 A의 몰수를 4 mol, 실험Ⅱ의 몰 수를 5 mol로 생각하여 풀어보자.
실험 I에서, 4 mol의 A와 반응한 B 6 g 이 모두 소진되었다. B 6 g을 3 mol이라 한다면, A는 2 mol이 반응하고, C와 D도 각각 2 mol이 생성되니 반응 후 전체기체 몰수/C몰수 = 3 도 만족한다. 남은 2 mol의 A 질량이 17w [g]에 해당한다고 볼 수 있다. A의 화학식량은 17w/2 [g/mol]이다.
반응한 A의 몰수가 k일 때, C몰수/반응후 전체 기체 = k / (4-k+k+k) = 1/3 , k =2
실험 II에서, 5 mol의 A가 모두 반응하면, B는 7.5 mol 반응해야 한다. 앞선 실험 I에서 B는 6 g = 3 mol에 해당했으므로, B의 분자량은 2 [g/mol]이다. B 7.5 mol = 15 g이다.
따라서 B 10 g이 남았다. 남은 B 10 [g] = 40w [g]이다. w = 1/4 이며, 앞선 A의 분자량은 17w/2 = 17/8 [g/mol]이 된다.
실험 II에서는 B 10 g (= 5 mol)이 남고, 생성되는 C와 D는 모두 5 mol씩이다. 따라서 반응 후 전체 기체 몰수/C몰수 = 3 으로 같다. x = 3 이다.
또한 실험 II의 생성된 D의 질량 = 45/8 [g]인데, 이것은 5 mol에 해당하므로, D의 분자량 = 45/40 = 9/8 [g/mol] 이다.
화학반응식을 통해 C의 분자량도 구할 수 있는데, 질량 보존에 따라 반응 전후 질량 2A + 3B = 2C + 2D 이기 때문이다.
2(17/8) + 3(2) = 2C + 2(9/8) 이며, 2C = (17/4) + 6 - (9/4) = 8 이며, C = 4 이다.
따라서, 문제에서 요구하는 x * (C/B) = 3 * (4/2) = 6 이다.
- 끝 -
* 위 문제의 출처는 한국교육과정평가원이며, 정답 및 해설 강의는 EBSi 사이트에서도 확인하실 수 있습니다.
