오스트발트 희석률 (Ostwald dilution law)
오스트발트 희석률 | Ostwald dilution law
0. 들어가기
오스트발트 희석률은 독일의 화학자 빌헬름 오스트발트(Friedrich Wilhelm Ostwald, 1853-1932)가 1888년 제안한 것으로 약산의 이온화 상수(Ka)와 약산의 이온화도 사이 관계를 나타낸 법칙을 말한다. (사실, 산-염기에만 국한된 것이 아닌, 수용액에서 해리되는 전해질들의 해리 상수 Kd 와 초기 농도 c0 , 전해질의 해리도(해리 분율) α 사이 관계에 대한 것이다.)


1. 유도하기
약산(약전해질)은 수용액에서 일부 해리되어 다음과 같은 평형 상태에 도달한다.

약산의 초기 농도를 c0, 약산의 이온화도를 α 라고 한다면,
약산은 이온화도의 비율만큼 해리되며, 해리된 약산의 농도는 c0*α 로 나타낼 수 있다. HA가 해리되는만큼, H+와 A-가 생성되므로, 생성된 H+와 A-의 농도 또한 c0*α 이다.

평형 상태에서의 약산의 농도는 c0 - c0*α 이며, 공통항인 c0로 묶어 c0(1 - α )와 같이 표현할 수 있다. 평형에서의 농도를 이온화 상수식에 대입하면, 다음과 같이 표현 가능하다.

매우 약한 전해질(약산, 약염기 등)의 경우 α 는 매우 작고, α ≒ 0 에 근사할 수 있으므로, 이온화 상수식의 1 - α ≒ 1 임을 뜻한다.

온도가 일정할 때, 산의 이온화 상수는 일정하므로, 약산의 이온화도(해리 정도)는 초기 농도 제곱근에 반비례한다. 다시 말해, 농도가 진할수록 약산의 이온화도(α )는 작아지며, 농도가 묽어질수록 이온화도(α )가 커진다.
2. 적용하기
0.1 M 아세트산(CH3COOH) 수용액의 이온화도(α )와 0.01 M 아세트산 수용액의 이온화도를 비교해보자. (단, 아세트산의 산 이온화 상수 Kd = 1.75 × 10-5 이다.
0.1 M 아세트산이 진한 용액, 0.01 M 아세트산을 상대적으로 묽은 용액이라 하자. 위에서 이끌어낸 결론에 그냥 대입해도 되지만 0.1 M 용액에 대하여 간략하게 풀이를 해보면,
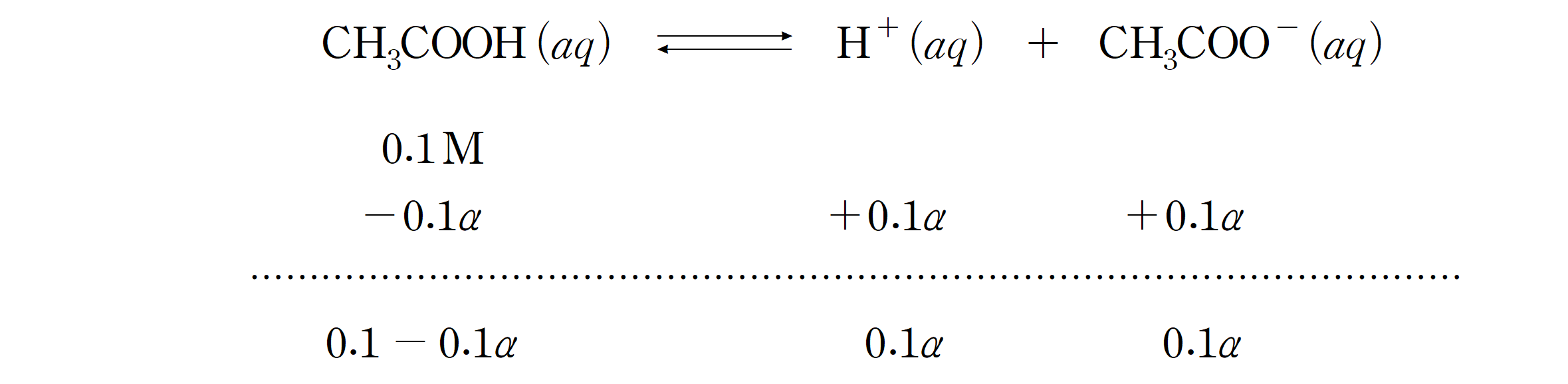
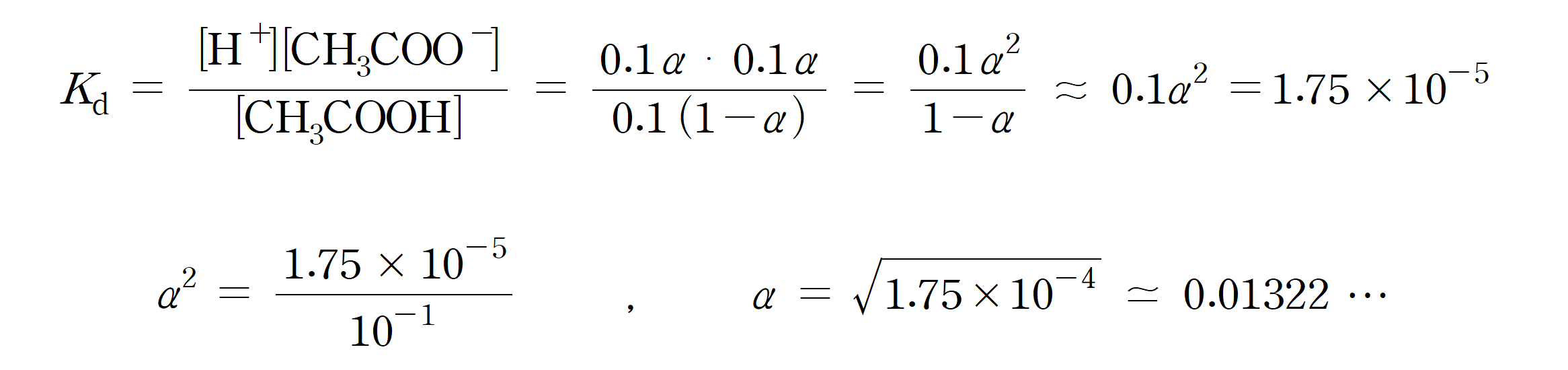
약, 1.32 %의 이온화도를 갖는 것을 알 수 있다.
같은 방법으로 10 배 묽은 0.01 M 아세트산 수용액의 이온화도를 구하면,
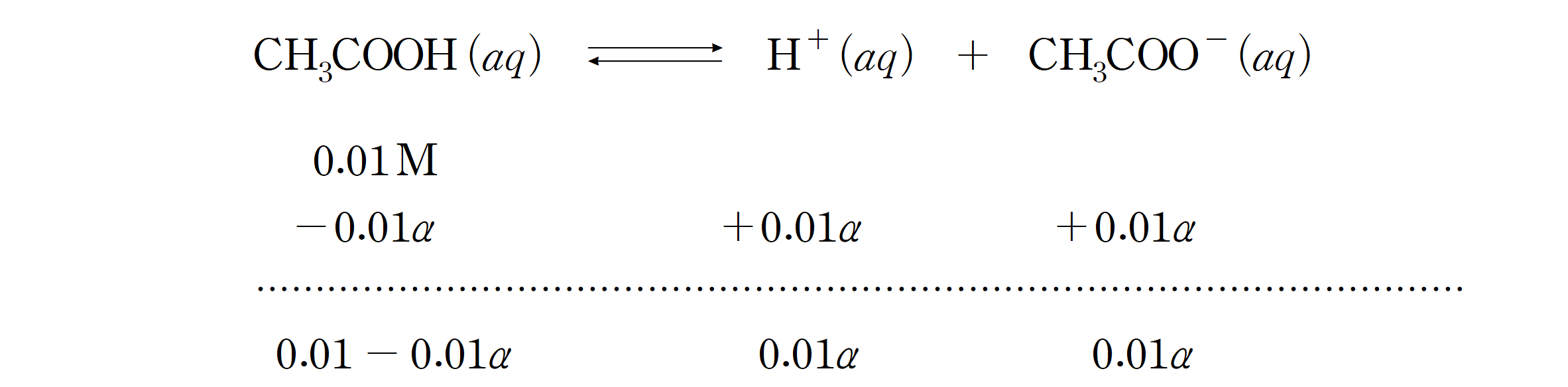
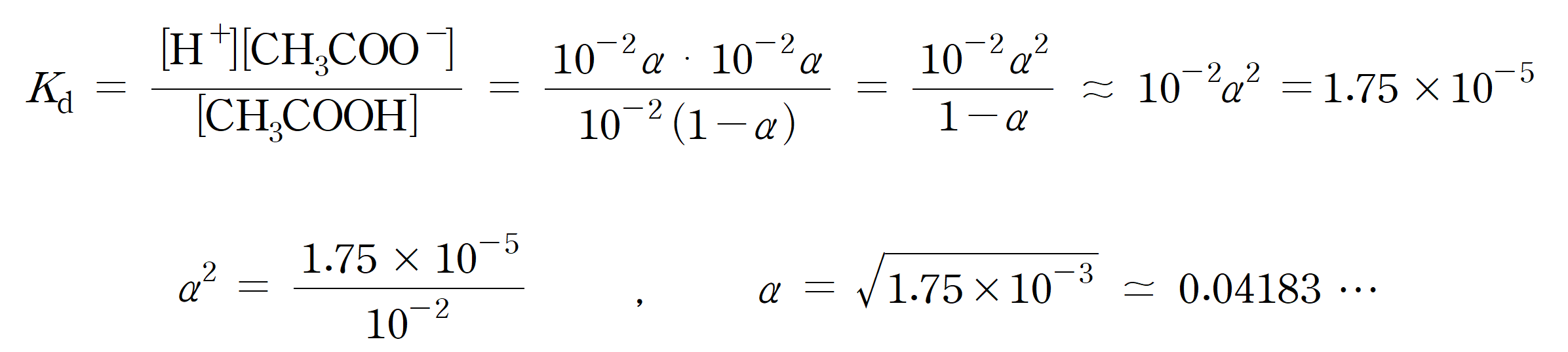
약 4.18%의 이온화도를 가지며, 0.1 M 수용액보다 약 2.86%의 이온화도가 증가했다. 농도가 묽은 용액일수록 이온화도(해리도)가 커짐을 확인할 수 있다.
3. 한계점
오스트발트 희석률은 일정 온도에서 산 또는 염기, 전해질의 해리 평형에서의 평형 상수 값이 일정함을 바탕으로 유도된다. 그러나 이온화도가 큰 강전해질, 강산-강염기의 경우 평형 상수 값이 일정치 않으며 이 법칙이 적용되지 않는다.
오스트발트 희석률
- 끝 -
* 끝까지 읽어주셔서 감사합니다.
[관련 글] 약산의 pH 구하기 https://stachemi.tistory.com/278
약산의 pH 구하기
약산의 pH 구하기 1. 산의 세기 이온화도(해리도)는 절대적 강산과 약산을 구분하는 척도가 된다. 이온화도는 산(HA)의 해리 분율에 관한 것으로 0 ~ 1 사이 값을 갖는다. 이온화도가 크다(1에 가깝
stachemi.tistory.com